题目内容
已知m=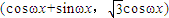 ,n=(cosωx-sinωx,2sinωx),其中ω>0,若函数f(x)=m•n,且f(x)的对称中心到f(x)对称轴的最近距离不小于
,n=(cosωx-sinωx,2sinωx),其中ω>0,若函数f(x)=m•n,且f(x)的对称中心到f(x)对称轴的最近距离不小于
(Ⅰ)求ω的取值范围;
(Ⅱ)在△ABC中,a,b,c分别是角A,B,C的对边,且a=1,b+c=2,当ω取最大值时,f(A)=1,求△ABC的面积.
【答案】分析:(Ⅰ)先将函数化简得:f(x)=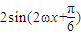 ,由于函数f(x)的周期
,由于函数f(x)的周期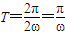 ,由题意知
,由题意知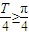 ,即
,即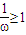 ,又ω>0,从而可确定ω的取值范围;
,又ω>0,从而可确定ω的取值范围;
(Ⅱ)由(I)知ω的最大值为1,所以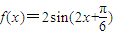 .利用f(A)=1,可求
.利用f(A)=1,可求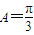 .由余弦定理可知:
.由余弦定理可知: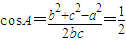 ,∴b2+c2-bc=1,又b+c=2,从而可求得:
,∴b2+c2-bc=1,又b+c=2,从而可求得: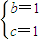 或
或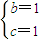 ,故可求△ABC的面积.
,故可求△ABC的面积.
解答:解:(Ⅰ)f(x)=m•n=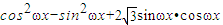 =
=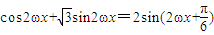 (3分)∵ω>0,∴函数f(x)的周期
(3分)∵ω>0,∴函数f(x)的周期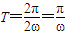 ,由题意知
,由题意知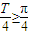 ,即
,即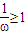 ,
,
又ω>0,∴0<ω≤1.故ω的取值范围是{ω|0<ω≤1}(6分)
(Ⅱ)由(I)知ω的最大值为1,∴ .
.
∵f(A)=1,∴ .而
.而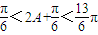 ,∴
,∴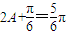 ,∴
,∴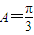 . (9分)
. (9分)
由余弦定理可知: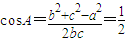 ,∴b2+c2-bc=1,又b+c=2.联立解得:
,∴b2+c2-bc=1,又b+c=2.联立解得: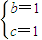 或
或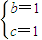 .
.
∴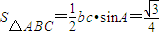 .(13分)
.(13分)
点评:本题主要考查例用辅助角公式转化成正弦型函数,考查余弦定理的运用及三角形的面积公式,有一定的综合性.
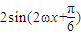 ,由于函数f(x)的周期
,由于函数f(x)的周期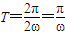 ,由题意知
,由题意知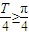 ,即
,即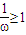 ,又ω>0,从而可确定ω的取值范围;
,又ω>0,从而可确定ω的取值范围;(Ⅱ)由(I)知ω的最大值为1,所以
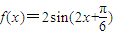 .利用f(A)=1,可求
.利用f(A)=1,可求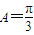 .由余弦定理可知:
.由余弦定理可知: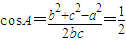 ,∴b2+c2-bc=1,又b+c=2,从而可求得:
,∴b2+c2-bc=1,又b+c=2,从而可求得: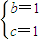 或
或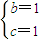 ,故可求△ABC的面积.
,故可求△ABC的面积.解答:解:(Ⅰ)f(x)=m•n=
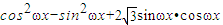 =
=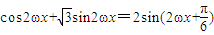 (3分)∵ω>0,∴函数f(x)的周期
(3分)∵ω>0,∴函数f(x)的周期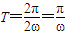 ,由题意知
,由题意知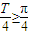 ,即
,即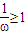 ,
,又ω>0,∴0<ω≤1.故ω的取值范围是{ω|0<ω≤1}(6分)
(Ⅱ)由(I)知ω的最大值为1,∴
 .
.∵f(A)=1,∴
 .而
.而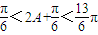 ,∴
,∴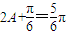 ,∴
,∴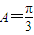 . (9分)
. (9分)由余弦定理可知:
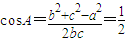 ,∴b2+c2-bc=1,又b+c=2.联立解得:
,∴b2+c2-bc=1,又b+c=2.联立解得: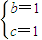 或
或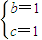 .
.∴
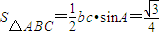 .(13分)
.(13分)点评:本题主要考查例用辅助角公式转化成正弦型函数,考查余弦定理的运用及三角形的面积公式,有一定的综合性.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案
相关题目