题目内容
【题目】已知定义在![]() 上的奇函数
上的奇函数![]() 满足
满足![]() .且当
.且当![]() 时,
时,![]() .若对于任意
.若对于任意![]() ,都有
,都有![]() ,则实数
,则实数![]() 的取值范围为________.
的取值范围为________.
【答案】![]()
【解析】
f(x)为周期为4的函数,且是奇函数.0在函数定义域内,故f(0)=0,得a=1,先得到[﹣1,3]一个周期内f(x)的图象,求出该周期内使f(x)≥1﹣log23成立的x的范围,从而推出![]() 的范围,再分t的范围讨论即可.
的范围,再分t的范围讨论即可.
解:由题意,f(x)为周期为4的函数,且是奇函数.0在函数定义域内,故f(0)=0,得a=1,
所以当0≤x≤1时,f(x)=log2(x+1),
当x∈[﹣1,0]时,﹣x∈[0,1],此时f(x)=﹣f(﹣x)=﹣log2(﹣x+1),
又知道f(x+2)=﹣f(x)=f(﹣x),
所以f(x)以x=1为对称轴.且当x∈[﹣1,1]时f(x)单调递增,
当x∈[1,3]时f(x)单调递减.
当x∈[﹣1,3]时,令f(x)=1﹣log23,得x![]() ,或x
,或x![]() ,
,
所以在[﹣1,3]内当f(x)>1﹣log23时,x∈[![]() ,
,![]() ].
].
设g(x)![]() ,若对于x属于[0,1]都有
,若对于x属于[0,1]都有![]() ,
,
因为g(0)![]() ∈[
∈[![]() ,
,![]() ].
].
故g(x)∈[![]() ,
,![]() ].
].
①当![]() 0时,g(x)在[0,1]上单调递减,
0时,g(x)在[0,1]上单调递减,
故g(x)∈[t![]() ,
,![]() ][
][![]() ,
,![]() ].得t≥0,无解.
].得t≥0,无解.
②0≤t≤1时,![]() ,此时g(t)最大,g(1)最小,
,此时g(t)最大,g(1)最小,
即g(x)∈[t﹣1,![]() ][
][![]() ,
,![]() ].得t∈[0,1].
].得t∈[0,1].
③当1<t≤2时,即![]() ,此时g(0)最小,g(t)最大,
,此时g(0)最小,g(t)最大,
即g(x)∈[![]() ,
,![]() ][
][![]() ,
,![]() ].得t∈(1,2],
].得t∈(1,2],
④当t>2时,g(x)在[0,1]上单调递增,
故g(x)∈[![]() ,t
,t![]() ][
][![]() ,
,![]() ].解得,t∈(2,3],
].解得,t∈(2,3],
综上t∈[0,3].
故填:[0,3].

 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案【题目】某小学为了解四年级学生的家庭作业用时情况,从本校四年级随机抽取了一批学生进行调查,并绘制了学生作业用时的频率分布直方图,如图所示.
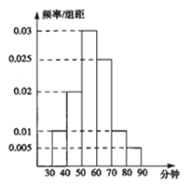
(1)估算这批学生的作业平均用时情况;
(2)作业用时不能完全反映学生学业负担情况,这与学生自身的学习习惯有很大关系如果用时四十分钟之内评价为优异,一个小时以上为一般,其它评价为良好.现从优异和良好的学生里面用分层抽样的方法抽取300人,其中女生有90人(优异20人).请完成列联表,并根据列联表分析能否在犯错误的概率不超过0.05的前提下认为学习习惯与性别有关系?
男生 | 女生 | 合计 | |
良好 | |||
优异 | |||
合计 |
附:![]() ,其中
,其中![]()
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |