��Ŀ����
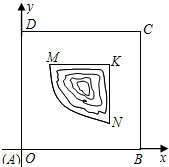
��ͼ��ij�½�С����һƬ�߳�Ϊ1����λ�����ף���������ʣ��ؿ�ABCD���м䲿��MNK��һƬ�����������ı�Ե���߶�MNΪ����y=
(
��x��
)��ͼ������ı�Ե��ƽ�������������ߵ�ֱ�߶Σ�Ϊ�������õؿ飬�ƻ���һ����Խ�õؿ��ֱ·�����Ȳ��ƣ���ֱ·l�����߶�MN���У��е��ΪP�������Ѹõؿ��Ϊ�����֣��ǵ�P����AD����Ϊt��f��t����ʾ�õؿ���ֱ·���²��ֵ������
��1����f��t���Ľ���ʽ��
��2�������S=f��t�������ֵ��
| 2 |
| 9x |
| 1 |
| 3 |
| 2 |
| 3 |
��1����f��t���Ľ���ʽ��
��2�������S=f��t�������ֵ��

��1����Ϊy=
������y��=-
����P��t��
����
���Թ���P�����߷���Ϊy-
=-
(x-t)����y=-
x+
��
��x=0����y=
����y=0����x=2t��
����������x�ύ��E��2t��0����������y�ύ��F(0��
)��
�ٵ�
����
��t��
ʱ���������·�������Ϊһֱ�������Σ�
����f(t)=
��2t��
=
��
�ڵ�
����
��t��
ʱ���������·�������Ϊһֱ�����Σ�
f(t)=
(
+
)•1=
��
�۵�
����
��t��
ʱ���������·�������Ϊһֱ�����Σ�
����f(t)=
(
+2t)•1=2t-
t2��
����f(t)=
��
��2����
��t��
ʱ��f(t)=2t-
t2=-
(t-
)2+
��
��
��
��t��
ʱ��f(t)=
=-
(
-2)2+
��
��
����Smax=
��
�������S=f��t�������ֵΪ
��
| 2 |
| 9x |
| 2 |
| 9x2 |
| 2 |
| 9t |
���Թ���P�����߷���Ϊy-
| 2 |
| 9t |
| 2 |
| 9t2 |
| 2 |
| 9t2 |
| 4 |
| 9t |
��x=0����y=
| 4 |
| 9t |
����������x�ύ��E��2t��0����������y�ύ��F(0��
| 4 |
| 9t |
�ٵ�
|
| 4 |
| 9 |
| 1 |
| 2 |
����f(t)=
| 1 |
| 2 |
| 4 |
| 9t |
| 4 |
| 9 |
�ڵ�
|
| 1 |
| 2 |
| 2 |
| 3 |
f(t)=
| 1 |
| 2 |
| 4 |
| 9t |
| 4t-2 |
| 9t2 |
| 4t-1 |
| 9t2 |
�۵�
|
| 1 |
| 3 |
| 4 |
| 9 |
����f(t)=
| 1 |
| 2 |
| 4t-9t2 |
| 2 |
| 9 |
| 4 |
����f(t)=
|
��2����
| 1 |
| 3 |
| 4 |
| 9 |
| 9 |
| 4 |
| 9 |
| 4 |
| 4 |
| 9 |
| 4 |
| 9 |
| 4 |
| 9 |
��
| 1 |
| 2 |
| 2 |
| 3 |
| 4t-1 |
| 9t2 |
| 1 |
| 9 |
| 1 |
| t |
| 4 |
| 9 |
| 4 |
| 9 |
����Smax=
| 4 |
| 9 |
�������S=f��t�������ֵΪ
| 4 |
| 9 |

��ϰ��ϵ�д�
 �ŵ������ϵ�д�
�ŵ������ϵ�д� 53������ϵ�д�
53������ϵ�д�
�����Ŀ
 �Ĵ�С��ϵΪ�� ��
�Ĵ�С��ϵΪ�� ��





 ��ͼ������ƽ��1����λ���ٽ�λ��
��ͼ������ƽ��1����λ���ٽ�λ�� ���·���ͼ����
���·���ͼ���� ��ͼ����ʵ��
��ͼ����ʵ�� ����
����
 ��
�� ��ֵ�ǣ� ��
��ֵ�ǣ� ��


