题目内容
设函数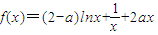 ;(a∈R).
;(a∈R).(1)当a=0时,求f(x)的极值.(2)当a≠0时,求f(x)的单调区间.(3)当a=2时,对于任意正整数n,在区间
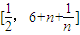 上总存在m+4个数a1,a2,a3,…,am,am+1,am+2,am+3,am+4,使得f(a1)+f(a2)+…+f(am)<f(am+1)+f(am+2)+f(am+3)+f(am+4)成立,试问:正整数m是否有最大值?若有求其最大值;否则,说明理由.
上总存在m+4个数a1,a2,a3,…,am,am+1,am+2,am+3,am+4,使得f(a1)+f(a2)+…+f(am)<f(am+1)+f(am+2)+f(am+3)+f(am+4)成立,试问:正整数m是否有最大值?若有求其最大值;否则,说明理由.
【答案】分析:(1)先求导函数为0的根,在看根左右两侧的符号,若左正右负,原函数取极大值;若左负右正,原函数取极小值.
(2)先求导函数,再求导函数为0的根,利用导函数大于0的区间为原函数的增区间,导函数小于0的区间为原函数的减区间来求单调区间即可.
(3)先判断出原函数在区间 上的单调性,再利用单调性把f(a1)+f(a2)+…+f(am)<f(am+1)+f(am+2)+f(am+3)+f(am+4)成立转化为
上的单调性,再利用单调性把f(a1)+f(a2)+…+f(am)<f(am+1)+f(am+2)+f(am+3)+f(am+4)成立转化为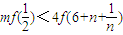 对一切正整数成立即可求出正整数m是否有最大值.
对一切正整数成立即可求出正整数m是否有最大值.
解答:解:(1)依题意,知f(x)的定义域为(0,+∞).
当a=0时,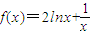 ,
,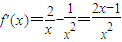 .
.
令f'(x)=0,解得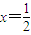 .
.
当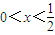 时,f'(x)<0;当
时,f'(x)<0;当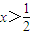 时,f'(x)>0.
时,f'(x)>0.
又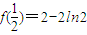 ,所以f(x)的极小值为2-2ln2,无极大值.
,所以f(x)的极小值为2-2ln2,无极大值.
(2)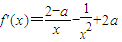 =
=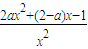 .
.
令f'(x)=0,解得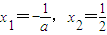 .
.
若a>0,令f'(x)<0,得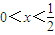 ;令f'(x)>0,得
;令f'(x)>0,得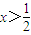 .
.
若a<0,
①当a<-2时,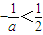 ,令f'(x)<0,得
,令f'(x)<0,得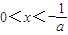 或
或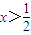 ;
;
令f'(x)>0,得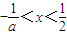 .
.
②当a=-2时,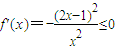 .
.
③当-2<a<0时,得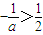 ,
,
令f'(x)<0,得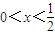 或
或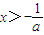 ;令f'(x)>0,得
;令f'(x)>0,得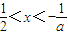 .
.
综上所述,当a>0时,f(x)的递减区间为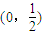 ,递增区间为
,递增区间为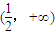 .
.
当a<-2时,f(x)的递减区间为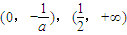 ;递增区间为
;递增区间为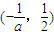 .
.
当a=-2时,f(x)递减区间为(0,+∞).
当-2<a<0时,f(x)的递减区间为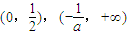 ,递增区间为
,递增区间为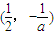 .
.
(3)当a=2时,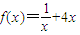 ,
,
由 ,知
,知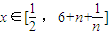 时,f'(x)≥0.
时,f'(x)≥0.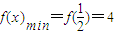 ,
,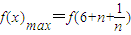 .
.
依题意得: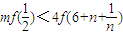 对一切正整数成立.
对一切正整数成立.
令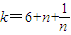 ,则k≥8(当且仅当n=1时取等号).
,则k≥8(当且仅当n=1时取等号).
又f(k)在区间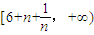 单调递增,得
单调递增,得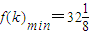 ,
,
故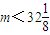 ,又m为正整数,得m≤32,
,又m为正整数,得m≤32,
当m=32时,存在 ,am+1=am+2=am+3=am+4=8,对所有n满足条件.所以,正整数m的最大值为32.
,am+1=am+2=am+3=am+4=8,对所有n满足条件.所以,正整数m的最大值为32.
点评:题考查利用导函数来研究函数的极值.在利用导函数来研究函数的极值时,分三步①求导函数,②求导函数为0的根,③判断根左右两侧的符号,若左正右负,原函数取极大值;若左负右正,原函数取极小值.
(2)先求导函数,再求导函数为0的根,利用导函数大于0的区间为原函数的增区间,导函数小于0的区间为原函数的减区间来求单调区间即可.
(3)先判断出原函数在区间
 上的单调性,再利用单调性把f(a1)+f(a2)+…+f(am)<f(am+1)+f(am+2)+f(am+3)+f(am+4)成立转化为
上的单调性,再利用单调性把f(a1)+f(a2)+…+f(am)<f(am+1)+f(am+2)+f(am+3)+f(am+4)成立转化为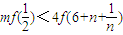 对一切正整数成立即可求出正整数m是否有最大值.
对一切正整数成立即可求出正整数m是否有最大值.解答:解:(1)依题意,知f(x)的定义域为(0,+∞).
当a=0时,
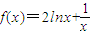 ,
,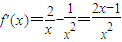 .
.令f'(x)=0,解得
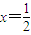 .
.当
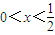 时,f'(x)<0;当
时,f'(x)<0;当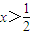 时,f'(x)>0.
时,f'(x)>0.又
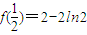 ,所以f(x)的极小值为2-2ln2,无极大值.
,所以f(x)的极小值为2-2ln2,无极大值.(2)
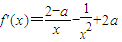 =
=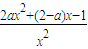 .
.令f'(x)=0,解得
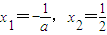 .
.若a>0,令f'(x)<0,得
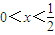 ;令f'(x)>0,得
;令f'(x)>0,得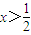 .
.若a<0,
①当a<-2时,
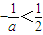 ,令f'(x)<0,得
,令f'(x)<0,得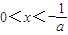 或
或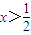 ;
;令f'(x)>0,得
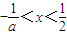 .
.②当a=-2时,
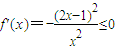 .
.③当-2<a<0时,得
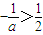 ,
,令f'(x)<0,得
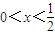 或
或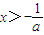 ;令f'(x)>0,得
;令f'(x)>0,得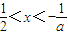 .
.综上所述,当a>0时,f(x)的递减区间为
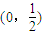 ,递增区间为
,递增区间为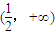 .
.当a<-2时,f(x)的递减区间为
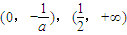 ;递增区间为
;递增区间为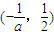 .
.当a=-2时,f(x)递减区间为(0,+∞).
当-2<a<0时,f(x)的递减区间为
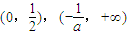 ,递增区间为
,递增区间为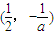 .
.(3)当a=2时,
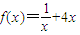 ,
,由
 ,知
,知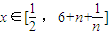 时,f'(x)≥0.
时,f'(x)≥0.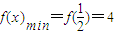 ,
,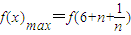 .
.依题意得:
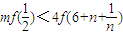 对一切正整数成立.
对一切正整数成立.令
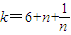 ,则k≥8(当且仅当n=1时取等号).
,则k≥8(当且仅当n=1时取等号).又f(k)在区间
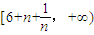 单调递增,得
单调递增,得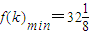 ,
,故
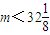 ,又m为正整数,得m≤32,
,又m为正整数,得m≤32,当m=32时,存在
 ,am+1=am+2=am+3=am+4=8,对所有n满足条件.所以,正整数m的最大值为32.
,am+1=am+2=am+3=am+4=8,对所有n满足条件.所以,正整数m的最大值为32.点评:题考查利用导函数来研究函数的极值.在利用导函数来研究函数的极值时,分三步①求导函数,②求导函数为0的根,③判断根左右两侧的符号,若左正右负,原函数取极大值;若左负右正,原函数取极小值.

练习册系列答案
相关题目
 ,其中a∈R,m是给定的正整数,且m≥2.如果不等式f(x)>(x-1)lgm在区间[1,+∞)上有解,则实数a的取值范围是 .
,其中a∈R,m是给定的正整数,且m≥2.如果不等式f(x)>(x-1)lgm在区间[1,+∞)上有解,则实数a的取值范围是 . ,其中a∈R,m是给定的正整数,且m≥2,如果不等式f(x)>(x-1)lgm在区间[1,+∞)有解,则实数a的取值范围是 .
,其中a∈R,m是给定的正整数,且m≥2,如果不等式f(x)>(x-1)lgm在区间[1,+∞)有解,则实数a的取值范围是 . ,其中a∈R,m是给定的正整数,且m≥2,如果不等式f(x)<(x-2)lgm在区间[1,+∞)上恒成立,则实数a的取值范围是 .
,其中a∈R,m是给定的正整数,且m≥2,如果不等式f(x)<(x-2)lgm在区间[1,+∞)上恒成立,则实数a的取值范围是 .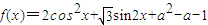 ,(a∈R)
,(a∈R)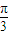 ]时,求f(x)的最大值.
]时,求f(x)的最大值.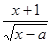 (a∈R),为使f(x)在区间(0,+∞)上为增函数,求a的取值范围。
(a∈R),为使f(x)在区间(0,+∞)上为增函数,求a的取值范围。