题目内容
(本大题满分10分)设函数f(x)=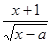 (a∈R),为使f(x)在区间(0,+∞)上为增函数,求a的取值范围。
(a∈R),为使f(x)在区间(0,+∞)上为增函数,求a的取值范围。
【答案】
a≤-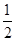
【解析】
试题分析:首先要使函数有意义,则a≤x。而考虑所给的题设,只需要最大限度地让函数在(0,+∞)有意义即可,所以a≤0。对f(x)求导并令其≥0,整理后得:[x-(2a+1)] 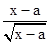 ≥0
≥0
由于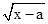 在a≤0时始终有意义且大于0,因此只需讨论[x-(2a+1)](x-a)≥0 .........①
在a≤0时始终有意义且大于0,因此只需讨论[x-(2a+1)](x-a)≥0 .........①
(1)若2a+1≥a,即a≥-1。①解为x≤a或x≥2a+1,所以令2a+1≤0即可,得到a≤-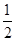
(2)若2a+1<a,即a<-1。①解为x<2a+1或x>a,所以令a≤0即可
综上所述,a的取值范围是(-∞,-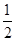 ]。
]。
考点:本题主要考查利用导数研究函数的单调性,一元二次不等式的解法。
点评:已知函数的单调区间,求参数,往往利用函数的导数不小于0。解答本题时,分类讨论是关键。

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目

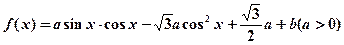 .
.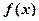 的单调递减区间;
的单调递减区间;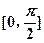 上的最小值是
上的最小值是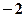 ,最大值是
,最大值是 ,求实数
,求实数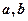 的值.
的值.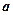 ,使函数
,使函数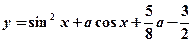 在闭区间
在闭区间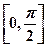 上的最大值为
上的最大值为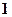 ?若存在,求出对应的
?若存在,求出对应的