题目内容
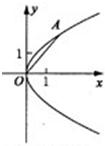 在平面直角坐标系xoy中,抛物线C的顶点在原点,经过点A(2,2),其焦点F在x轴上.
在平面直角坐标系xoy中,抛物线C的顶点在原点,经过点A(2,2),其焦点F在x轴上.(1)求抛物线C的标准方程;
(2)求过点F,且与直线OA垂直的直线的方程;
(3)设过点M(m,0)(m>0)的直线交抛物线C于D、E两点,ME=2DM,记D和E两点间的距离为f(m),求f(m)关于m的表达式.
分析:(1)先设出抛物线的方程,把点A代入即可求得p,则抛物线的方程可得.
(2)根据(1)中抛物线的方程求得焦点的坐标,利用A点求得OA的斜率,进而求得其垂线的斜率,利用点斜式求得其方程.
(3)设出D,E的坐标和直线DE的方程,代入抛物线方程求得交点纵坐标,利用ME=2DM进而等式求得k和m的关系式,进而利用两点间的距离公式表示出DE的长,把m和k的关系式代入即可.
(2)根据(1)中抛物线的方程求得焦点的坐标,利用A点求得OA的斜率,进而求得其垂线的斜率,利用点斜式求得其方程.
(3)设出D,E的坐标和直线DE的方程,代入抛物线方程求得交点纵坐标,利用ME=2DM进而等式求得k和m的关系式,进而利用两点间的距离公式表示出DE的长,把m和k的关系式代入即可.
解答: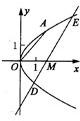 解:(1)由题意,可设抛物线的标准方程为y2=2px,
解:(1)由题意,可设抛物线的标准方程为y2=2px,
因为点A(2,2),在抛物线上,所以p=1,
抛物线的标准方程为y2=2x
(2)由(1)可得焦点F坐标是(
,0),又直线AO的斜率为
=1,
故与直线OA垂直的直线的斜率为-1,
因此所求直线的方程为x+y-
=0
(3)设点D和E的坐标分别是(x1,y1)和(x2,y2),直线DE的方程是y=k(x-m).
k≠0,将x=
+m代入抛物线方程有ky2-2y-2km=0,解得y1,2=
由ME=2DM知1+
=2(
-1),化简得k2=
,
∴DE2=(x1-x2)2+(y1-y2)2=
(m2+4m)
所以f(m)=
(m>0)
 解:(1)由题意,可设抛物线的标准方程为y2=2px,
解:(1)由题意,可设抛物线的标准方程为y2=2px,因为点A(2,2),在抛物线上,所以p=1,
抛物线的标准方程为y2=2x
(2)由(1)可得焦点F坐标是(
| 1 |
| 2 |
| 2 |
| 2 |
故与直线OA垂直的直线的斜率为-1,
因此所求直线的方程为x+y-
| 1 |
| 2 |
(3)设点D和E的坐标分别是(x1,y1)和(x2,y2),直线DE的方程是y=k(x-m).
k≠0,将x=
| y |
| k |
1±
| ||
| k |
由ME=2DM知1+
| 1+2mk2 |
| 1+2mk2 |
| 4 |
| m |
∴DE2=(x1-x2)2+(y1-y2)2=
| 9 |
| 4 |
所以f(m)=
| 3 |
| 2 |
| m2+4m |
点评:本小题主要考查直线、抛物线及两点间的距离公式等基本知识,考查运算求解能力.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
 如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是
如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是