题目内容
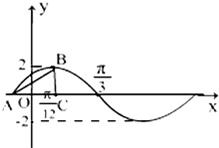已知f（x）=2sin（ωx+φ），（ω＞0，-| π |
| 2 |
| π |
| 2 |
| π |
| 12 |
| AB |
| BC |
A、
| ||
B、
| ||
| C、4 | ||
| D、-4 |
分析：由题意求出T，利用周期公式求出ω，利用当x=
时取得最大值2，求出φ，得到函数的解析式，然后求出A的坐标，得到
和
然后求出
•
即可．
| π |
| 12 |
| AB |
| BC |
然后求出
| AB |
| BC |
解答：解：由题意可知T=4×(
-
)=π，ω=2，
当x=
时取得最大值2，
所以2=2sin（2×
+φ），φ=
，
所以函数解析式为f（x）=2sin（2x+
），
A的坐标为（-
，0），B（
，2）
=（
，2）
=（0，-2）
•
=（
，2）•（0，-2）=-4
故答案为：-4
| π |
| 3 |
| π |
| 12 |
当x=
| π |
| 12 |
所以2=2sin（2×
| π |
| 12 |
| π |
| 3 |
所以函数解析式为f（x）=2sin（2x+
| π |
| 3 |
A的坐标为（-
| π |
| 6 |
| π |
| 12 |
| AB |
| π |
| 4 |
| BC |
| AB |
| BC |
| π |
| 4 |
故答案为：-4
点评：本题是基础题，考查由y=Asin（ωx+φ）的部分图象确定其解析式，注意函数的周期的求法，考查计算能力，数量积的计算，常考题型．
练习册系列答案
相关题目
（2011•孝感模拟）已知f（x）=2sin（ωx+φ）的部分图象如图所示，则f（x）的表达式为（ ）