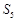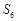题目内容
已知在递增等差数列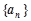 中,
中,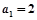 ,
,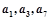 成等比数列,数列
成等比数列,数列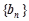 的前n项和为
的前n项和为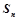 ,且
,且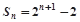 .
.
(1)求数列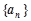 、
、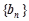 的通项公式;(2)设
的通项公式;(2)设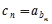 ,求数列
,求数列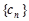 的前
的前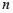 和
和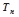 .
.
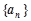 中,
中,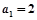 ,
,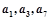 成等比数列,数列
成等比数列,数列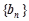 的前n项和为
的前n项和为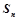 ,且
,且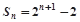 .
.(1)求数列
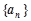 、
、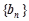 的通项公式;(2)设
的通项公式;(2)设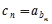 ,求数列
,求数列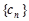 的前
的前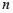 和
和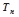 .
.(1)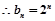
(2)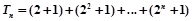
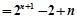
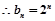
(2)
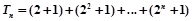
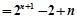
本题主要考查了利用基本量表示的等差数列、等比数列的通项,求和公式的应用,错位相减求解数列的和,属于数列的知识的综合应用.
(1)根据已知条件可知三项的关系式,利用通项公式得到结论。
(2)根据第一问的结论得到通项公式,然后运用分组求和得到结论
(1)因为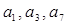 成等比数列,
成等比数列,
所以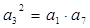 .设等差数列
.设等差数列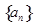 的公差为
的公差为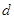 ,则
,则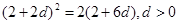 .,得到d=1,然后求解得到结论。同时
.,得到d=1,然后求解得到结论。同时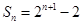 ,
,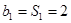
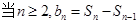 ,得到其通项公式。
,得到其通项公式。
(2)因为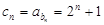 ,然后运用分组求和法得到结论。
,然后运用分组求和法得到结论。
解:(1)因为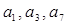 成等比数列,
成等比数列,
所以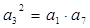 . ……………………1分
. ……………………1分
设等差数列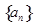 的公差为
的公差为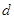 ,则
,则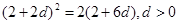 . ………2分
. ………2分
所以d=1 ………3分
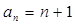 . ………4分
. ………4分
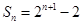 ,
,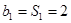 ………5分
………5分
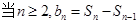 ,………6分
,………6分
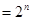 ……7分
……7分
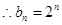 ………8分
………8分
(2)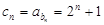 ………9分
………9分
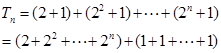 ………11分
………11分
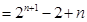 ………14分
………14分
(1)根据已知条件可知三项的关系式,利用通项公式得到结论。
(2)根据第一问的结论得到通项公式,然后运用分组求和得到结论
(1)因为
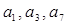 成等比数列,
成等比数列,所以
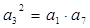 .设等差数列
.设等差数列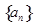 的公差为
的公差为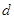 ,则
,则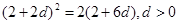 .,得到d=1,然后求解得到结论。同时
.,得到d=1,然后求解得到结论。同时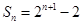 ,
,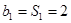
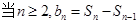 ,得到其通项公式。
,得到其通项公式。(2)因为
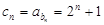 ,然后运用分组求和法得到结论。
,然后运用分组求和法得到结论。解:(1)因为
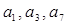 成等比数列,
成等比数列,所以
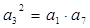 . ……………………1分
. ……………………1分设等差数列
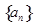 的公差为
的公差为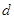 ,则
,则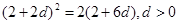 . ………2分
. ………2分所以d=1 ………3分
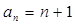 . ………4分
. ………4分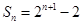 ,
,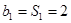 ………5分
………5分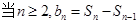 ,………6分
,………6分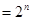 ……7分
……7分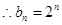 ………8分
………8分(2)
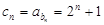 ………9分
………9分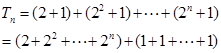 ………11分
………11分 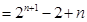 ………14分
………14分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
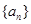 是公比大于1的等比数列,
是公比大于1的等比数列,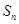 为数列
为数列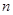 项和。
项和。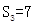 ,且
,且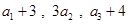 构成等差数列.
构成等差数列.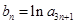 ,求数列
,求数列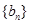 的前
的前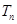 .
.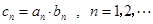 ,求数列
,求数列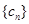 的前
的前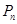 .
.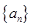 的前
的前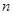 项和为
项和为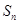 ,若
,若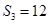 ,且
,且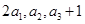 成等比数列.
成等比数列.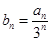 的前
的前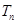 ,求证
,求证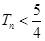 .
.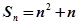 ,那么它的通项公式为an=_________
,那么它的通项公式为an=_________ 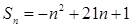 ,
,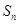 的最大值,并求出相应的
的最大值,并求出相应的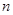 的值.
的值.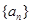 中,公差
中,公差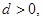 又
又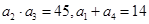 .
.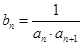 ,数列
,数列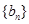 的前
的前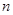 项和记为
项和记为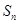 ,求
,求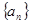 的前
的前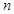 项和为
项和为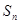 ,且
,且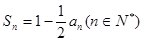
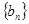 的通项公式
的通项公式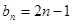 ,记
,记 ,求数列
,求数列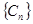 的前
的前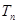 .
.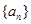 中,若
中,若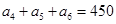 ,则
,则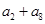 的值为 .
的值为 .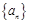 是等差数列,
是等差数列,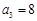 ,
,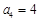 ,则前
,则前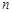 项和
项和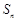 中最大的是( )
中最大的是( )
 或
或