题目内容
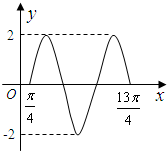 (2012•济南三模)函数f(x)=2sin(ωx+φ)的图象,其部分图象如图所示,则f(0)=
(2012•济南三模)函数f(x)=2sin(ωx+φ)的图象,其部分图象如图所示,则f(0)=-
| 2 |
-
.| 2 |
分析:利用函数的图象求出函数的周期,求出ω,通过函数x=
函数值为0,求出?,得到函数的解析式,然后求出f(0)的值.
| π |
| 4 |
解答:解:由图象可知
T=
-
=3π,所以T=2π,
所以T=2π=
,所以ω=1,即函数为f(x)=2sin(x+),
由五点对应法可知,当x=
时,有
+?=0,所以?=-
,
所以f(x)=2sin(x-
),
所以f(0)=2sin(-
)=-
.
故答案为:-
| 3 |
| 2 |
| 13π |
| 4 |
| π |
| 4 |
所以T=2π=
| 2π |
| ω |
由五点对应法可知,当x=
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
所以f(x)=2sin(x-
| π |
| 4 |
所以f(0)=2sin(-
| π |
| 4 |
| 2 |
故答案为:-
| 2 |
点评:本题考查三角函数的解析式的求法,三角函数的图象的应用,考查视图能力与计算能力.

练习册系列答案
相关题目
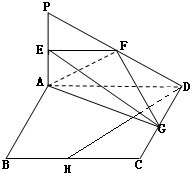 (2012•济南三模)如图所示,PA⊥平面ABCD,四边形ABCD为正方形,且2PA=AD,E、F、G、H分别是线段PA、PD、CD、BC的中点.
(2012•济南三模)如图所示,PA⊥平面ABCD,四边形ABCD为正方形,且2PA=AD,E、F、G、H分别是线段PA、PD、CD、BC的中点.