题目内容
(本小题满分12分)
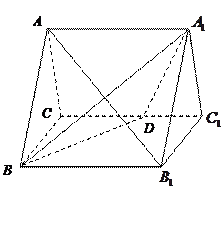 如图,正三棱柱
如图,正三棱柱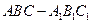 的所有棱长都为
的所有棱长都为
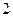 ,
,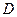 为
为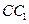 中点.
中点.
(Ⅰ)求证: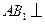 平面
平面 ;
;
(Ⅱ)求二面角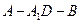 的大小;
的大小;
(Ⅲ)求点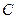 到平面
到平面 的距离.
的距离.
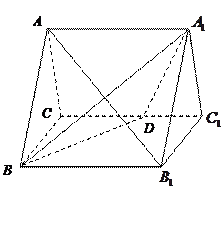 如图,正三棱柱
如图,正三棱柱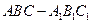 的所有棱长都为
的所有棱长都为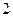 ,
,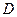 为
为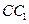 中点.
中点.(Ⅰ)求证:
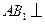 平面
平面 ;
;(Ⅱ)求二面角
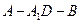 的大小;
的大小;(Ⅲ)求点
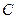 到平面
到平面 的距离.
的距离.(Ⅰ)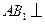 平面
平面
(Ⅱ)二面角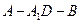 的大小为
的大小为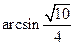
(Ⅲ)点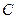 到平面
到平面 的距离为
的距离为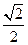
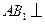 平面
平面
(Ⅱ)二面角
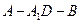 的大小为
的大小为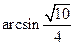
(Ⅲ)点
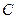 到平面
到平面 的距离为
的距离为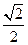
解法一:(Ⅰ)取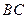 中点
中点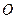 ,连结
,连结 .
.
 为正三角形,
为正三角形, .
.
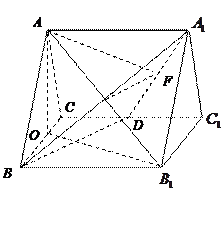
 正三棱柱
正三棱柱 中,平面
中,平面 平面
平面 ,
,
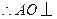 平面
平面 .
.
连结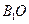 ,在正方形
,在正方形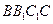 中,
中, 分别为
分别为
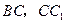 的中点,
的中点,
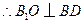 ,
,
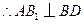 .
.
在正方形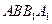 中,
中,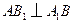 ,
,
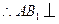 平面
平面 .
.
(Ⅱ)设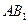 与
与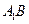 交于点
交于点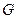 ,在平面
,在平面 中,作
中,作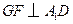 于
于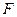 ,连结
,连结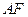 ,由(Ⅰ)得
,由(Ⅰ)得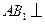 平面
平面 .
.
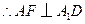 ,
,
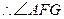 为二面角
为二面角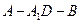 的平面角.
的平面角.
在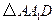 中,由等面积法可求得
中,由等面积法可求得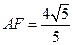 ,
,
又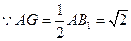 ,
,
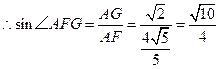 .
.
所以二面角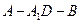 的大小为
的大小为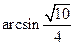 .
.
(Ⅲ)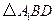 中,
中,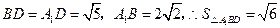 ,
, .
.
在正三棱柱中,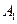 到平面
到平面 的距离为
的距离为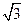 .
.
设点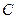 到平面
到平面 的距离为
的距离为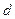 .
.
由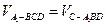 得
得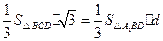 ,
,
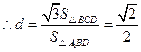 .
.
 点
点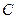 到平面
到平面 的距离为
的距离为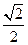 .
.
解法二:(Ⅰ)取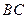 中点
中点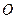 ,连结
,连结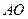 .
.
 为正三角形,
为正三角形, .
.
 在正三棱柱
在正三棱柱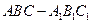 中,平面
中,平面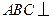 平面
平面 ,
,
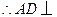 平面
平面 .
.
取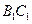 中点
中点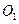 ,以
,以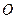 为原点,
为原点,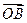 ,
,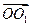 ,
,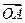 的方向为
的方向为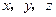 轴的正方向建立空间直角坐标系,则
轴的正方向建立空间直角坐标系,则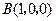 ,
, ,
,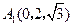 ,
,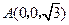 ,
,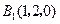 ,
,
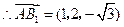 ,
,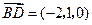 ,
,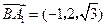 .
.
 ,
,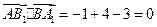 ,
,
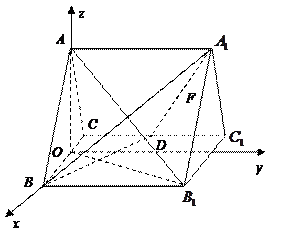
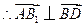 ,
,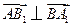 .
.
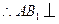 平面
平面 .
.
(Ⅱ)设平面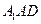 的法向量为
的法向量为 .
.
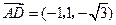 ,
,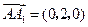 .
.
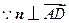 ,
,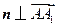 ,
,
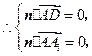
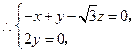
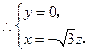
令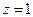 得
得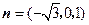 为平面
为平面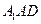 的一个法向量.
的一个法向量.
由(Ⅰ)知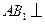 平面
平面 ,
,
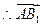 为平面
为平面 的法向量.
的法向量.
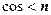 ,
,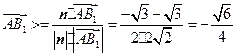 .
.
 二面角
二面角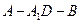 的大小为
的大小为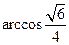 .
.
(Ⅲ)由(Ⅱ),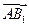 为平面
为平面 法向量,
法向量,
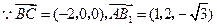 .
.
 点
点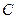 到平面
到平面 的距离
的距离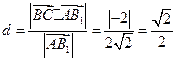
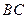 中点
中点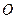 ,连结
,连结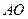 .
. 为正三角形,
为正三角形, .
.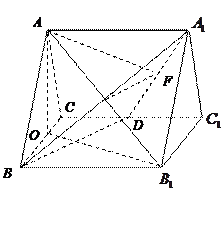
 正三棱柱
正三棱柱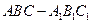 中,平面
中,平面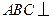 平面
平面 ,
,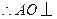 平面
平面 .
.连结
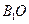 ,在正方形
,在正方形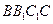 中,
中, 分别为
分别为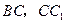 的中点,
的中点,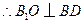 ,
,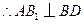 .
.在正方形
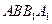 中,
中,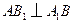 ,
,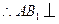 平面
平面 .
.(Ⅱ)设
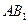 与
与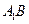 交于点
交于点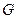 ,在平面
,在平面 中,作
中,作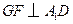 于
于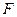 ,连结
,连结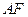 ,由(Ⅰ)得
,由(Ⅰ)得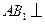 平面
平面 .
.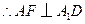 ,
,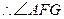 为二面角
为二面角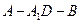 的平面角.
的平面角.在
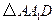 中,由等面积法可求得
中,由等面积法可求得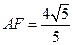 ,
,又
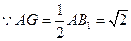 ,
,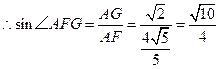 .
.所以二面角
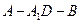 的大小为
的大小为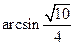 .
.(Ⅲ)
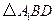 中,
中,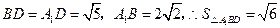 ,
, .
.在正三棱柱中,
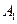 到平面
到平面 的距离为
的距离为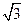 .
.设点
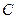 到平面
到平面 的距离为
的距离为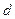 .
.由
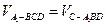 得
得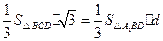 ,
,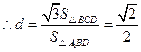 .
.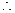 点
点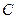 到平面
到平面 的距离为
的距离为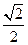 .
.解法二:(Ⅰ)取
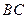 中点
中点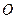 ,连结
,连结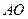 .
. 为正三角形,
为正三角形, .
. 在正三棱柱
在正三棱柱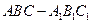 中,平面
中,平面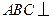 平面
平面 ,
,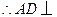 平面
平面 .
.取
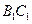 中点
中点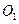 ,以
,以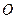 为原点,
为原点,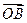 ,
,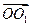 ,
,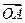 的方向为
的方向为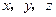 轴的正方向建立空间直角坐标系,则
轴的正方向建立空间直角坐标系,则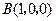 ,
, ,
,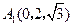 ,
,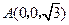 ,
,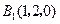 ,
,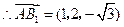 ,
,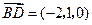 ,
,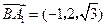 .
. ,
,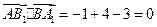 ,
,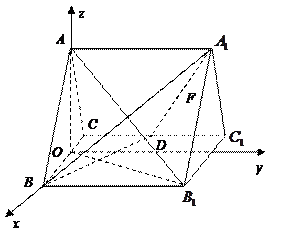
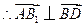 ,
,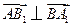 .
.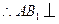 平面
平面 .
.(Ⅱ)设平面
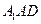 的法向量为
的法向量为 .
.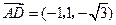 ,
,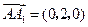 .
.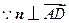 ,
,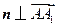 ,
,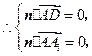
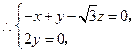
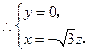
令
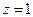 得
得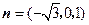 为平面
为平面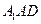 的一个法向量.
的一个法向量.由(Ⅰ)知
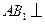 平面
平面 ,
,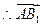 为平面
为平面 的法向量.
的法向量.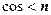 ,
,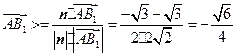 .
. 二面角
二面角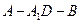 的大小为
的大小为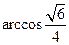 .
.(Ⅲ)由(Ⅱ),
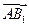 为平面
为平面 法向量,
法向量,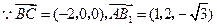 .
.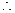 点
点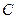 到平面
到平面 的距离
的距离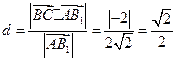

练习册系列答案
相关题目

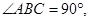
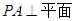 ,
,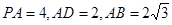 ,BC=6.
,BC=6.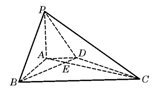
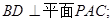
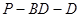 的大小.
的大小.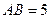 ,AA1=4,点D是AB的中点.
,AA1=4,点D是AB的中点.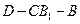 的平面角的正切值.
的平面角的正切值.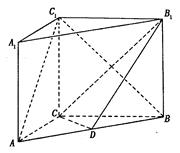
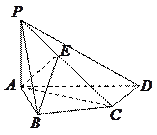
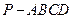 中,
中,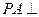 底面
底面 ,
,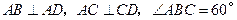 ,
,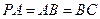 ,
,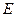 是
是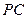 的中点.
的中点.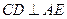 ;
;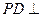 平面
平面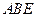 ;
;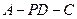 的大小.
的大小.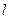 为一条直线,
为一条直线,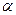 、
、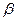 、
、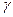 为三个互不重合的平面,给出下面三个语句:
为三个互不重合的平面,给出下面三个语句: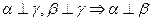 ②
②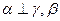 //
//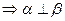
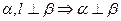
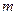 、
、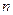 与平面
与平面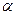 、
、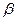 ,给出下列三个命题( )
,给出下列三个命题( )
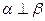 ;其中真命题的个数是:
;其中真命题的个数是:
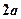 的正方体容器被水充满,首先把半径为
的正方体容器被水充满,首先把半径为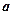 的球放入其中,再放入一个能被水完全淹没的小球,若想使溢出的水量最大,这个小球的半径为( )
的球放入其中,再放入一个能被水完全淹没的小球,若想使溢出的水量最大,这个小球的半径为( )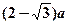
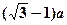
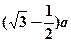
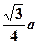
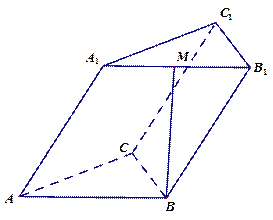
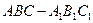 的底面是正三角形,侧面
的底面是正三角形,侧面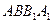 是边长为2的菱形,
是边长为2的菱形,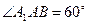 ,
,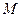 是
是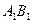 的中点,
的中点,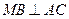 .
.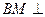 平面
平面 ;
; 的距离.
的距离.