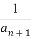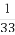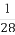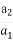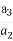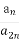题目内容
设数列{an}的前n项和为Sn,已知a1=1,Sn+1=2Sn+n+1(n∈N*),则数列{an}的通项公式an= .
2n-1
【解析】∵Sn+1=2Sn+n+1,当n≥2时Sn=2Sn-1+n,
两式相减得:an+1=2an+1,
∴an+1+1=2(an+1),
即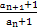 =2.
=2.
又S2=2S1+1+1,a1=S1=1,
∴a2=3,∴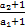 =2,
=2,
∴{an+1}是首项为2,公比为2的等比数列,
∴an+1=2n即an=2n-1(n∈N*).
【方法技巧】含Sn,an问题的求解策略
当已知含有Sn+1,Sn之间的等式时,或者含有Sn,an的混合关系的等式时,可以采用降级角标或者升级角标的方法再得出一个等式,两个等式相减就把问题转化为数列的通项之间的递推关系式.

练习册系列答案
相关题目