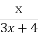题目内容
已知各项都不相等的等差数列{an}的前6项和为60,且a6为a1和a21的等比中项.
(1)求数列{an}的通项公式.
(2)若数列{bn}满足bn+1-bn=an(n∈N*),且b1=3,求数列{ }的前n项和Tn.
}的前n项和Tn.
(1) an=2n+ (2) Tn=
【解析】(1)设等差数列{an}的公差为d(d≠0),
则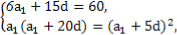
解得 ∴an=2n+3.
∴an=2n+3.
(2)由bn+1-bn=an,
∴bn-bn-1=an-1(n≥2,n∈N*),
bn=(bn-bn-1)+(bn-1-bn-2)+…+(b2-b1)+b1
=an-1+an-2+…+a1+b1=n(n+2),
当n=1时,b1=3也适合上式,
∴bn=n(n+2)(n∈N*).
∴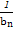 =
=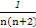 =
= (
( -
- ),
),
Tn= (1-
(1- +
+ -
-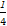 +…+
+…+ -
- )
)
= (
( -
- -
- )=
)= .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目