题目内容
满足sin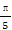 sinx+cos
sinx+cos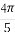 cosx=
cosx= 的锐角x= .
的锐角x= .
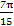
【解析】原式可化为cos(x- )=
)=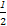 ,
,
∴x- =±
=± +2kπ(k∈Z).
+2kπ(k∈Z).
∵x为锐角,∴x=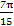 .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
满足sin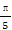 sinx+cos
sinx+cos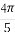 cosx=
cosx= 的锐角x= .
的锐角x= .
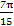
【解析】原式可化为cos(x- )=
)=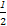 ,
,
∴x- =±
=± +2kπ(k∈Z).
+2kπ(k∈Z).
∵x为锐角,∴x=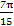 .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案