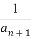题目内容
已知二次函数f(x)=px2+qx(p≠0),其导函数为f'(x)=6x-2,数列{an}的前n项和为Sn,点(n,Sn)(n∈N*)均在函数y=f(x)的图象上.
(1)求数列{an}的通项公式.
(2)若cn= (an+2),2b1+22b2+23b3+…+2nbn=cn,求数列{bn}的通项公式.
(an+2),2b1+22b2+23b3+…+2nbn=cn,求数列{bn}的通项公式.
(1) an=6n-5 (2) bn=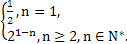
【解析】【思路点拨】(1)根据二次函数的导函数为f'(x)=6x-2,可求f(x)=3x2-2x,所以Sn=3n2-2n.由Sn可求an.
(2)根据an求cn,求出cn代入2b1+22b2+23b3+…+2nbn=cn中可求出bn,注意n=1与n≥2的讨论.
【解析】
(1)已知二次函数f(x)=px2+qx(p≠0),
则f'(x)=2px+q=6x-2,故p=3,q=-2,
所以f(x)=3x2-2x.
点(n,Sn)(n∈N*)均在函数y=f(x)的图象上,
则Sn=3n2-2n,当n=1时,a1=S1=1;
当n≥2时,an=Sn-Sn-1=6n-5,
故数列{an}的通项公式:an=6n-5.
(2)由(1)得,cn=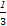 (an+2)=2n-1,
(an+2)=2n-1,
2b1+22b2+23b3+…+2nbn=2n-1,
当n=1时,b1=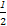 ,
,
当n≥2时,2b1+22b2+23b3+…+2n-1bn-1+2nbn
=2n-1,
2b1+22b2+23b3+…+2n-1bn-1=2(n-1)-1,
两式相减得:bn=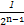 =21-n,
=21-n,
故数列{bn}的通项公式:bn=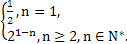

练习册系列答案
相关题目