Question

已知椭圆

x2

a2

+

y2

b2

=1（a＞b＞0）的左、右顶点分别A、B，椭圆过点（0，1）且离心率e=

3

2

．
（1）求椭圆的标准方程；
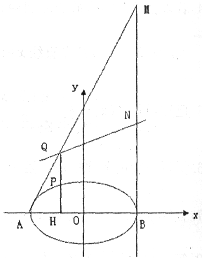
（2）过椭圆上异于A，B两点的任意一点P作PH⊥x轴，H为垂足，延长HP到点Q，且PQ=HP，过点B作直线l⊥x轴，连结AQ并延长交直线l于点M，N为MB的中点，试判断直线QN与以AB为直径的圆O的位置关系．

Answer 1

分析：（1）由题意得到b，然后结合离心率及条件a²=b²+c²求得a，则椭圆方程可求；
（2）设出P点的坐标及Q点的坐标，由HP=PQ得到两点坐标的关系，把P的坐标代入椭圆方程可得Q点的轨迹方程，写出直线AQ的方程，取x=2得到M的坐标，由中点坐标公式求出N的坐标，得到向量

OQ

，

NQ

的坐标，求其数量积即可得到答案．

解答：解：（1）因为椭圆经过点（0，1），所以b=1，又椭圆的离心率e=

3

2

得

c

a

=

3

2

，
即3a²=4c²，由a²=b²+c²得a²=1+c²，所以a=2，
故所求椭圆方程为

x2

4

+y2=1；
（2）直线QN与圆O相切．
事实上，设P（x₀，y₀），则

x02

4

+y02=1，设Q（x，y），∵HP=PQ，∴x=x₀，y=2y₀
即x0=x，y0=

1

2

y，将（x₀，y₀）代入

x02

4

+y02=1，得x²+y²=4，
所以Q点在以O为圆心，2为半径的圆上，即Q点在以AB为直径的圆O上．
又A（-2，0），直线AQ的方程为y=

2y0

x0+2

(x+2)，令x=2，则M(2，

8y0

x0+2

)，
又B（2，0），N为MB的中点，∴N(2，

4y0

x0+2

)，

OQ

=(x0，2y0)，

NQ

=(x0-2，

2x0y0

x0+2

)
∴

OQ

•

NQ

=x0(x0-2)+2y0•

2x0y0

x0+2

=x0(x0-2)+

4x0y02

x0+2

=x₀（x₀-2）+x₀（2-x₀）=0，∴

OQ

⊥

NQ

，∴直线QN与圆O相切．

点评：本题考查了椭圆方程的求法，考查了直线与圆锥曲线的关系，训练了利用向量的数量积判断垂直关系，体现了“设而不求”的解题思想方法，属难题．