题目内容
设x1,x2∈R,常数a>0,定义运算“*”:x1*x2=(x1+x2)2-(x1-x2)2,若x≥0,则动点P(x,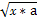 )的轨迹是( )
)的轨迹是( )
| A.圆 | B.椭圆的一部分 |
| C.双曲线的一部分 | D.抛物线的一部分 |
D
解析

练习册系列答案
相关题目
抛物线 上的一点M到焦点的距离为1,则点M到y轴的距离是( )
上的一点M到焦点的距离为1,则点M到y轴的距离是( )
A. | B. | C.1 | D. |
已知0<θ< ,则双曲线C1:
,则双曲线C1: -
- =1与C2:
=1与C2: -
- =1的( )
=1的( )
| A.实轴长相等 | B.虚轴长相等 |
| C.离心率相等 | D.焦距相等 |
已知点A(2,0),抛物线C:x2=4y的焦点为F,射线FA与抛物线C相交于点M,与其准线相交于点N,则|FM|∶|MN|等于( )
A.2∶ | B.1∶2 | C.1∶ | D.1∶3 |
已知抛物线方程为y2=4x,直线l的方程为x-y+4=0,在抛物线上有一动点P到y轴的距离为d1,P到直线l的距离为d2,则d1+d2的最小值为( )
A. +2 +2 | B. +1 +1 | C. -2 -2 | D. -1 -1 |
已知任意k∈R,直线y-kx-1=0与椭圆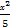 +
+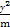 =1恒有公共点,则实数m的取值范围是( )
=1恒有公共点,则实数m的取值范围是( )
| A.(0,1) | B.(0,5) |
| C.[1,5)∪(5,+∞) | D.[1,5) |
设抛物线y2=8x上一点P到y轴的距离是4,则点P到该抛物线焦点的距离是( )
| A.4 | B.6 | C.8 | D.12 |
已知双曲线 =1的一个焦点与抛物线y2=4
=1的一个焦点与抛物线y2=4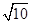 x的焦点重合,且双曲线的离心率等于
x的焦点重合,且双曲线的离心率等于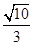 ,则该双曲线的方程为( )
,则该双曲线的方程为( )
A.x2-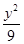 =1 =1 | B.x2-y2=15 |
C.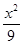 -y2=1 -y2=1 | D.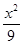 - -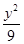 =1 =1 |
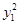 +
+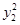 的最小值是( )
的最小值是( )