题目内容
13.若|$\overrightarrow{a}$|=3,与|$\overrightarrow{b}$|=2,向量$\overrightarrow{a}$与$\overrightarrow{b}$之间夹角为60°,且(3$\overrightarrow{a}$+5$\overrightarrow{b}$)⊥(m$\overrightarrow{a}$-$\overrightarrow{b}$),则实数m=( )| A. | $\frac{23}{32}$ | B. | $\frac{23}{43}$ | C. | $\frac{29}{42}$ | D. | $\frac{21}{10}$ |
分析 运用向量的数量积的定义,通过向量$\overrightarrow{a}$与$\overrightarrow{b}$的数量积,再由向量垂直的条件,列出方程,化简整理即可求出m.
解答 解:∵|$\overrightarrow{a}$|=3,与|$\overrightarrow{b}$|=2,向量$\overrightarrow{a}$与$\overrightarrow{b}$之间夹角为60°,且(3$\overrightarrow{a}$+5$\overrightarrow{b}$)⊥(m$\overrightarrow{a}$-$\overrightarrow{b}$),
∴(3$\overrightarrow{a}$+5$\overrightarrow{b}$)•(m$\overrightarrow{a}$-$\overrightarrow{b}$)=3m${\overrightarrow{a}}^{2}$$+(5m-3)\overrightarrow{a}•\overrightarrow{b}$$-{5\overrightarrow{b}}^{2}$=0,27m+(5m-3)×$3×2×\frac{1}{2}$-20=0,
∴42m-29=0,
∴m=$\frac{29}{42}$.
故选:C.
点评 本题考查向量的数量积的定义,向量垂直的条件,考查基本的运算能力,属于基础题.

练习册系列答案
相关题目
18.若角α的终边经过点$(\sqrt{5},-2)$,则sinα等于多少( )
| A. | $\frac{2}{3}$ | B. | $\frac{{\sqrt{5}}}{3}$ | C. | $-\frac{2}{3}$ | D. | $-\frac{{\sqrt{5}}}{3}$ |
5.下图所示的圆锥的俯视图为( )
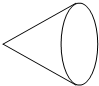

| A. | 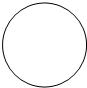 | B. | 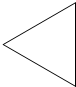 | C. |  | D. |  |