题目内容
设数列 的前
的前 项和为
项和为 ,已知
,已知 (
( ,
, 为常数),
为常数), ,
, ,(1)求数列
,(1)求数列 的通项公式;(2)求所有满足等式
的通项公式;(2)求所有满足等式 成立的正整数
成立的正整数 ,
, .
.
(1)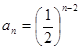 (
( );(2)
);(2)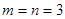 .
.
解析试题分析:(1)由 取n=1,及
取n=1,及  ,
, ,可求得
,可求得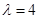 ,再由
,再由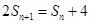 构造两个关系相减求得
构造两个关系相减求得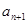 与
与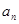 关系,进而知道
关系,进而知道 为等比数列,从而可求得通项公式;(2)由(1),得
为等比数列,从而可求得通项公式;(2)由(1),得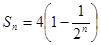 ,代入
,代入 ,同时注意变形技巧,易得n与m的关系,注意到
,同时注意变形技巧,易得n与m的关系,注意到 ,
, 为正整数,以m为分类标准进行讨论,进而求得n与m的值.
为正整数,以m为分类标准进行讨论,进而求得n与m的值.
试题解析:(1)由题意,得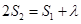 ,求得
,求得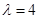 .所以,
.所以,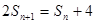 ①
①
当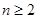 时,
时,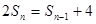 ②
②
①-②,得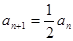 (
(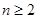 ),又
),又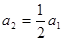 ,所以数列
,所以数列 是首项为
是首项为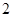 ,公比为
,公比为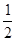 的等比数列,
的等比数列,
故 的通项公式为
的通项公式为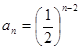 (
( ).
).
(2)由(1),得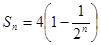 ,由
,由 ,两边倒数,且有
,两边倒数,且有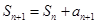 ,因此得
,因此得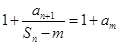 ,化简得
,化简得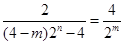 ,即
,即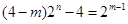 ,即
,即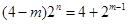 .(*)因为
.(*)因为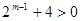 ,所以
,所以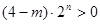 ,所以
,所以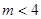 ,因为
,因为 ,所以
,所以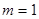 或
或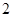 或
或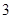 .
.
当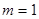 时,由(*)得
时,由(*)得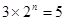 ,所以无正整数解;
,所以无正整数解;
当 时,由(*)得
时,由(*)得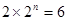 ,所以无正整数解;
,所以无正整数解;
当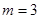 时,由(*)得
时,由(*)得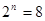 ,所以
,所以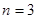 .综上可知,存在符合条件的正整数
.综上可知,存在符合条件的正整数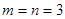 .
.
考点:1,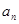 与
与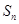 的关系:
的关系: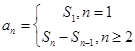 ;2,等比数列通项公式,前n项和公式;3,分类讨论思想.
;2,等比数列通项公式,前n项和公式;3,分类讨论思想.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
 的前
的前 项和为
项和为 ,若
,若 ,则
,则 .
. 的首项
的首项 .
. 是等比数列,并求出
是等比数列,并求出 ;
; .
. 的前n项和
的前n项和 与通项
与通项 满足
满足 .
. ,求
,求 ;
; ,求
,求 的前n项和
的前n项和 .
. 的首项
的首项 ,且
,且
 .
. 的前
的前 项和
项和 .
. 的前
的前 项和
项和 .
. ,都有
,都有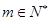 ,使得
,使得 成等比数列.
成等比数列. }中,
}中,
 }是等比数列,并求出数列{
}是等比数列,并求出数列{ 项和
项和 ,则常数
,则常数