题目内容
已知数列 的前n项和
的前n项和 与通项
与通项 满足
满足 .
.
(1)求数列 的通项公式;
的通项公式;
(2)设 ,求
,求 ;
;
(3)若 ,求
,求 的前n项和
的前n项和 .
.
(1) ;(2)
;(2)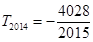 ;(3)
;(3)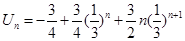 .
.
解析试题分析:(1)条件中 是前
是前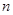 项和
项和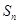 与第
与第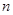 项
项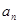 之间的关系,考虑到当
之间的关系,考虑到当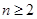 时,
时,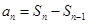 ,因此可得
,因此可得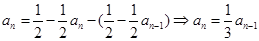 ,又由
,又由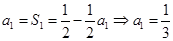 ,从而可以证明数列
,从而可以证明数列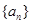 是以
是以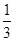 为首项,
为首项,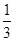 为公比的等比数列,∴通项公式
为公比的等比数列,∴通项公式 ;(2)由(1)结合
;(2)由(1)结合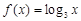 ,可得
,可得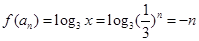 ,
,
从而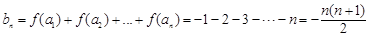 ,因此考虑采用裂项相消法求
,因此考虑采用裂项相消法求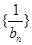 的前
的前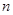 项和,即有
项和,即有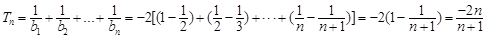 ;(3)由(2)及
;(3)由(2)及 ,可得
,可得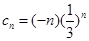 ,因此
,因此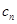 可看作是一个等比数列与一个等差数列的积,可以考虑采用错位相减法求其前
可看作是一个等比数列与一个等差数列的积,可以考虑采用错位相减法求其前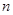 项和,即有
项和,即有 ①,
①,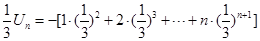 ②,
②,
①-②: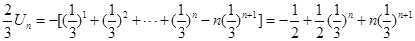 ,
,
从而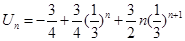 .
.
(1)在 中,令
中,令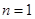 ,可得
,可得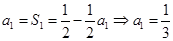 ..............2分
..............2分
当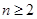 时,
时,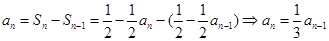 ,
,
∴数列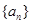 是以
是以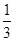 为首项,
为首项,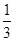 为公比的等比数列,∴
为公比的等比数列,∴ ; 4分
; 4分
由(1)及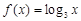 ,∴
,∴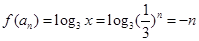 ,
,
∴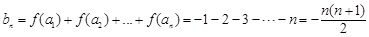 ,故
,故 ,..............6分
,..............6分
又∵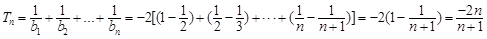 ,...... 9分
,...... 9分
∴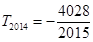 10分
10分
(3)由(2)及 ,∴
,∴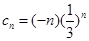 , 12分
, 12分
∴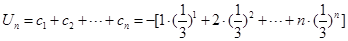 ①,
①,
①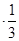 可得:
可得: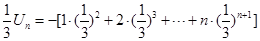 ②,
②,
①-②: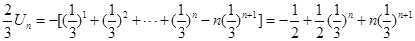 ,
,
∴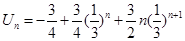 , 16分
, 16分
考点:1.求数列的通项公式;2裂项消法求数列的和;3.错位相减法求数列的和.

练习册系列答案
 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
 中,若
中,若 ,则
,则 的
的 的各项均为正数,且
的各项均为正数,且 .
. ,求数列
,求数列 的前
的前 项和
项和 .
. 是公比为
是公比为 的等比数列,推导
的等比数列,推导 项公式.
项公式. 的前
的前 项和为
项和为 ,已知
,已知 (
( ,
, 为常数),
为常数), ,
, ,(1)求数列
,(1)求数列 成立的正整数
成立的正整数 ,
, 满足
满足 .
. 是等比数列,并求数列
是等比数列,并求数列 ;
; ,数列
,数列 的前
的前 项和为
项和为 ,求证:对任意
,求证:对任意 ,有
,有 成立.
成立. 的首项
的首项 。
。 是等比数列,并求出
是等比数列,并求出 ;
;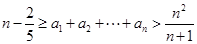 。
。 ,定义
,定义 它的第
它的第 项为
项为
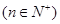 ,假设
,假设 是首项是
是首项是 公比为
公比为 的等比数列.
的等比数列. 的前
的前 ;
; ,
, ,
, .
. ;
; .
. 项和
项和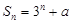 ,则常数
,则常数