��Ŀ����
����Ŀ��(1)��ѡ��4��1������֤��ѡ��
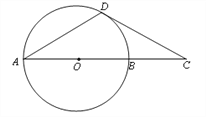
��ͼ��CD��ԲO�����ߣ��е�ΪD��CA�ǹ�Բ��O�ĸ����ҽ�ԲO�ڵ�B��DA��DC����֤�� CA��3CB��
(2)��ѡ��4��2��������任
�������A��![]() ��
��
������A��1��
����������C�ھ���A��Ӧ�ı任�����µõ�����C��6x2��y2��1��������C�ķ��̣�
(3)��ѡ��4��4������ϵ���������
��ƽ��ֱ������ϵxOy�У�ֱ��l�IJ�������Ϊ![]() ��tΪ��������ԲC�IJ�������Ϊ
��tΪ��������ԲC�IJ�������Ϊ![]() ����Ϊ����������ֱ��l��ԲC���У���ʵ��a��ֵ��
����Ϊ����������ֱ��l��ԲC���У���ʵ��a��ֵ��
(4)��ѡ��4��5������ʽѡ��
�ⲻ��ʽ��|x��2|��|x��1|��5��
���𰸡���1����������2������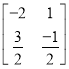 ����8y2��3x2��1��3��1��
����8y2��3x2��1��3��1��![]() ��4��(���ޣ���2]��[3������).
��4��(���ޣ���2]��[3������).
�������������������1������![]() ��
�� ![]() ,
, ![]() ΪԲ
ΪԲ![]() �����ߣ�
�����ߣ� ![]() �� �Ӷ�
�� �Ӷ�![]() ,�ɵ�
,�ɵ�![]() �������ɵý������2������
�������ɵý������2������![]() ������һ��
������һ��![]() �ھ���
�ھ���![]() ��Ӧ�ı任�����µõ���
��Ӧ�ı任�����µõ���![]() ��
�� ![]() ������
������![]() �����ɵý������3������ֱ��
�����ɵý������3������ֱ��![]() ����ͨ������Բ
����ͨ������Բ![]() ����ͨ���̣�����Բ�ĵ�ֱ�ߵľ�����ڰ뾶�ɵý������4��������������ۣ��ֱ���ⲻ��ʽ�飬Ȼ�������ɵý��.
����ͨ���̣�����Բ�ĵ�ֱ�ߵľ�����ڰ뾶�ɵý������4��������������ۣ��ֱ���ⲻ��ʽ�飬Ȼ�������ɵý��.
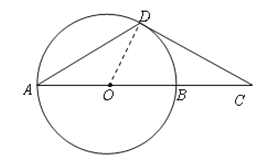
�����������1��֤��������OD����ΪDA=DC��
���ԡ�DAO=��C��
��ԲO�У�AO=DO�����ԡ�DAO=��ADO��
���ԡ�DOC=2��DAO=2��C��
��ΪCDΪԲO�����ߣ����ԡ�ODC=90�㣬
�Ӷ�DOC��C��90�㣬
��2��C����C��90�㣬�ʡ�C��30�㣬
����OC��2OD��2OB��
����CB��OB������CA��3CB��
��2�������������ʽ���ɵ�A��1��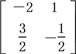 ��
��
����������C������һ��P(x��y)�ھ���A��Ӧ�ı任�����µõ���P (x��y)��
��![]() ��
��![]()
![]() ��
��![]() ������
������![]()
��Ϊ(x��y)������C�ϣ�����6x2��y2��1������6(x��2y)2��(3x��4y)2��1�������8y2��3x2��1��
��������C�ķ���Ϊ8y2��3x2��1
��3����ֱ��l�IJ�������Ϊ![]() ����ֱ��l����ͨ����Ϊx��y��1��0��
����ֱ��l����ͨ����Ϊx��y��1��0��
��ԲC�IJ�������Ϊ![]() ����ԲC����ͨ����Ϊ(x��a)2+(y��2a)2��1��
����ԲC����ͨ����Ϊ(x��a)2+(y��2a)2��1��
��Ϊֱ��l��ԲC���У�����![]() ��1��
��1��
���a��1��![]() ��
��
����ʵ��a��ֵΪ1��![]() ��
��
��4��(1)��x����1ʱ������ʽ�ɻ�Ϊ��x��2��x��1��5�����x�ܣ�2��
(2)����1��x��2ʱ������ʽ�ɻ�Ϊ��x��2��x��1��5����ʱ����ʽ�⣻
(3)��x��2ʱ������ʽ�ɻ�Ϊx��2��x��1��5�����x��3��
����ԭ����ʽ�Ľ⼯Ϊ(���ޣ���2]��[3������).

����Ŀ������������ָ��ҵ��У������վ�㡢����վ�㡢����������ҵ�����������������ṩ���г��������������ǹ������õ�һ������̬.һ������������ҵ��ij�����о͡�һ����һ��������ƽ���ɱ�����λ��Ԫ�������õ�������������λ��ǧ����֮��Ĺ�ϵ�����е����о����ڵ�������н�����ͳ�ƣ��ó�������ݼ��±���
���õ������� | 2 | 3 | 4 | 5 | 8 |
ÿ��һ����ƽ���ɱ� | 3.2 | 2.4 | 2 | 1.9 | 1.7 |
�����������ݣ��о���Ա�ֱ�����ס������ֲ�ͬ�Ļع�ģ�ͣ��õ������ع鷽�̣����̼ף� ![]() �������ң�
�������ң� ![]() .
.
(1)Ϊ����������ģ�͵����Ч��,�����������:
������±�(��������ȷ��0.1)(��ע: ![]() ,
,![]() ��Ϊ��Ӧ�ڵ�
��Ϊ��Ӧ�ڵ�![]() �IJв�(Ҳ��������));
�IJв�(Ҳ��������));
���õ������� | 2 | 3 | 4 | 5 | 8 | |
ÿ��һ����ƽ���ɱ� | 3.2 | 2.4 | 2 | 1.9 | 1.7 | |
ģ�ͼ� | ����ֵ | 2.4 | 2.1 | 1.6 | ||
�в� | 0 | -0.1 | 0.1 | |||
ģ���� | ����ֵ | 2.3 | 2 | 1.9 | ||
�в� | 0.1 | 0 | 0 | |||
�ڷֱ����ģ�ͼ���ģ���ҵIJв�ƽ����![]() ��
��![]() ,��ͨ���Ƚ�
,��ͨ���Ƚ�![]() �Ĵ�С,�ж��ĸ�ģ�����Ч������.
�Ĵ�С,�ж��ĸ�ģ�����Ч������.
(2)�����˾�ڸó���Ͷ�Ź����������ܵ������������һ�ӭ������������������Ӧ�����Ǹù�˾�о��Ƿ�����Ͷ��.�����г����飬�������Ͷ��8ǧ��ʱ���ù�˾ƽ��һ������һ��������10Ԫ��6Ԫ����ĸ��ʷֱ�Ϊ0.6��0.4��Ͷ��1����ʱ���ù�˾ƽ��һ������һ��������10Ԫ��6Ԫ����ĸ��ʷֱ�Ϊ0.4��0.6.�ʸù�˾Ӧ��Ͷ��8ǧ������1�����ܻ�ø�����������1�������Ч���Ϻõ�ģ�ͼ���һ����һ��������ƽ���ɱ�������=����-�ɱ���.