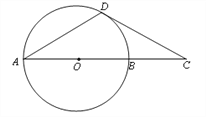
��Ŀ����
����Ŀ����֪����f��x��=x+ ![]() ��x��0��m��0���ͺ���g��x��=a|x��b|+c��x��R��a��0��b��0�����ʣ�
��x��0��m��0���ͺ���g��x��=a|x��b|+c��x��R��a��0��b��0�����ʣ�
��1��֤����f��x���ڣ� ![]() ��+�ޣ�������������
��+�ޣ�������������
��2���Ѻ���g1��x��=|x|��g2��x��=|x��1|д�ɷֶκ�������ʽ�����������ǵ�ͼ���ܽ��g2��x����ͼ���������g1��x����ͼ��õ��ģ�������������Ľ���˵����g��x����ͼ�����x=b�Գƣ�
��3����m=1��b=2��c=0ʱ����f��x����g��x�����������x��0���������a��ȡֵ��Χ��
���𰸡�
��1��֤������ ![]() ����ȡ����ʵ��x1��x2����x1��x2�����x=x2��x1��0��
����ȡ����ʵ��x1��x2����x1��x2�����x=x2��x1��0�� ![]() ��
��
��Ϊ ![]() ��
�� ![]() ������x1x2��m��0������x2��x1��0�����ԡ�y��0��
������x1x2��m��0������x2��x1��0�����ԡ�y��0��
����f��x���� ![]() ��������
��������
��2���⣺ ![]() ��
�� ![]() ��
��
g2��x����ͼ������g1��x����ͼ������ƽ��1����λ�õ��ģ�
�ȿ��Ǻ���h��x��=a|x|+c��x��R��b��0����
��h��x���Ķ���������ȡһ��ʵ��x����xҲ���䶨�����ڣ�
��Ϊh����x��=a|��x|+c=a|x|+c=h��x�������Ժ���h��x����ż������
����ͼ��ĶԳ���Ϊx=0��
���������ۣ�g��x����ͼ������h��x����ͼ������ƽ��b����λ�õ���
����g��x����ͼ�����x=b�Գƣ�
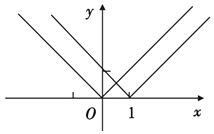
��3���⣺�������֪ ![]() ���������x��0�������
���������x��0�������
��x��2ʱ������ʽ��Ϊ ![]() ��
��
����a��1��x2��2ax��1��0��������x��2�������
��a��1=0ʱ����a=1������ʽ��Ϊ2x+1��0���������⣻
��a��1��0ʱ�������� ![]() �����Գ���
�����Գ��� ![]() ��
��
���ԣ�a��1��22��2a2��1��0�����0��a��1��
��������������0��a��1��
��0��x��2ʱ������ʽ ![]() ��
��
����a+1��x2��2ax+1��0��������0��x��2�������
������ ![]() �����Գ���
�����Գ��� ![]() ��
��
���ԡ�=4a2��4��a+1����0����a2��a��1��0����� ![]() ��
��
���� ![]() ��
��
����������a��ȡֵ��ΧΪ��0��1]��
����������1�����ú��������ԵĶ����ֱ��֤��f��x���� ![]() ��������������2��������֪g2��x����ͼ������g1��x����ͼ������ƽ��1����λ�õ��ģ����ݺ�����������ƽ�ƿ�֤��g��x����ͼ�����x=b�Գƣ���3������ת��˼�룺�������֪
��������������2��������֪g2��x����ͼ������g1��x����ͼ������ƽ��1����λ�õ��ģ����ݺ�����������ƽ�ƿ�֤��g��x����ͼ�����x=b�Գƣ���3������ת��˼�룺�������֪ ![]() ���������x��0���������x��2ʱ������ʽ��Ϊ
���������x��0���������x��2ʱ������ʽ��Ϊ ![]() ��
��
����a��1��x2��2ax��1��0��������x��2�������
�����㾫�����������õ����о������ĵ������ǽ����ĸ�������Ҫ֪��һ���,�����ĵ��������䵼�������������¹�ϵ�� ��ij������![]() �ڣ�(1)���
�ڣ�(1)���![]() ����ô����
����ô����![]() ��������䵥��������(2)���
��������䵥��������(2)���![]() ����ô����
����ô����![]() ��������䵥���ݼ���
��������䵥���ݼ���

����Ŀ��ij���������ף�������оƬ��������������ָ�껮��Ϊ��ָ����ڻ����82Ϊ�ϸ�Ʒ��С��82Ϊ��Ʒ���������ȡ������оƬ��100�����м�⣬�����ͳ�����£�
����ָ�� | [70��76�� | [76��82�� | [82��88�� | [88��94�� | [94��100] |
оƬ�� | 8 | 12 | 40 | 32 | 8 |
оƬ�� | 7 | 18 | 40 | 29 | 6 |
��1���Էֱ����оƬ�ף�оƬ��Ϊ�ϸ�Ʒ�ĸ��ʣ�
��2������һ��оƬ�ף����Ǻϸ�Ʒ��ӯ��40Ԫ�����Ǵ�Ʒ�����5Ԫ������һ��оƬ�ң����Ǻϸ�Ʒ��ӯ��50Ԫ�����Ǵ�Ʒ�����10Ԫ���ڣ�1����ǰ���£���XΪ����1��оƬ��1��оƬ�����õ����������������X�ķֲ��м�����1��оƬ��1��оƬ�������������ƽ��ֵ��