题目内容
设命题p:函数f(x)=lg(ax2-x+
a)的定义域为R;命题q:3x-9x<a对一切的实数均成立,如果命题“p或q”为真命题,且“p且q”为假命题,求实数a的取值范围.
| 1 |
| 16 |
∵命题p:函数f(x)=lg(ax2-x+
a)的定义域为R,
∴ax2-x+
a>0恒成立,
显然,a≠0,
∴
,解得a>2;
∵命题q:3x-9x<a对一切的实数均成立,令g(x)=3x-9x,
则a>g(x)max.
∵g(x)=3x-9x=-(3x-
)2+
≤
,
∴g(x)max=
,
∴a>
.
∵“p或q”为真命题,且“p且q”为假命题,
∴命题p与命题q一真一假.
若p真q假,则a∈∅;
若p假q真,即
,则
<a≤2.
综上所述,
<a≤2.
故答案为:
<a≤2.
| 1 |
| 16 |
∴ax2-x+
| 1 |
| 16 |
显然,a≠0,
∴
|
∵命题q:3x-9x<a对一切的实数均成立,令g(x)=3x-9x,
则a>g(x)max.
∵g(x)=3x-9x=-(3x-
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
∴g(x)max=
| 1 |
| 4 |
∴a>
| 1 |
| 4 |
∵“p或q”为真命题,且“p且q”为假命题,
∴命题p与命题q一真一假.
若p真q假,则a∈∅;
若p假q真,即
|
| 1 |
| 4 |
综上所述,
| 1 |
| 4 |
故答案为:
| 1 |
| 4 |

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
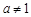 .设命题
.设命题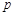 :函数
:函数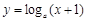 在(0,+∞)上单调递减,命题
在(0,+∞)上单调递减,命题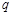 :曲线
:曲线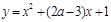 与x轴交于不同的两点,如果
与x轴交于不同的两点,如果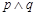 是假命题,
是假命题,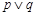 是真命题,求a的取值范围.
是真命题,求a的取值范围.