题目内容
长方体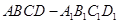 的各个顶点都在表面积为
的各个顶点都在表面积为 的球
的球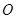 的球面上,其中
的球面上,其中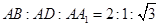 ,则四棱锥
,则四棱锥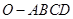 的体积为( )
的体积为( )
A.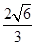 | B. | C.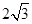 | D.3 |
A
解析试题分析:因为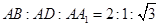 ,故可设AB、AD、AA1分别为2x,x,
,故可设AB、AD、AA1分别为2x,x, x,(x>0)
x,(x>0)
由题意可知,长方体ABCD-A1B1C1D1的体对角线等于其外接球O的直径,而由S=4πR2=16π,
得R=2,即2R=4,故4= ,解得,x=
,解得,x=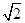
,故三边长分别为2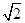 ,
,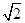 ,
,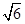 。
。
即四棱锥O-ABCD的底面为边长为2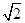 ,
,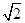 的矩形,高为
的矩形,高为
∴四棱锥O-ABCD的体积V=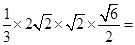
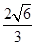 。故选A。
。故选A。
考点:本题主要考查长方体、球、正四棱锥的几何性质。
点评:中档题,作为长方体与外接球的问题,长方体的体对角线等于其外接球O的直径是解决问题的关键。

练习册系列答案
相关题目
已知m,n为两条不同的直线,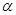 、
、 为两个不同的平面,则下列命题中正确的是
为两个不同的平面,则下列命题中正确的是
A.若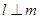  , ,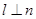  ,且 ,且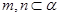  ,则 ,则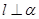  |
B.若平面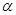  内有不共线的三点到平面 内有不共线的三点到平面  的距离相等,则 的距离相等,则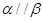  |
C.若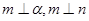  ,则 ,则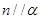  |
D.若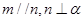  ,则 ,则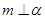 |
设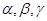 是三个互不重合的平面,m,n是两条不重合的直线,则下列命题中正确的是( )
是三个互不重合的平面,m,n是两条不重合的直线,则下列命题中正确的是( )
A. | B.若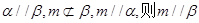 |
C.若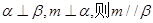 | D.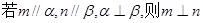 |
若 是空间中互不相同的直线,
是空间中互不相同的直线,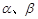 是不重合的两平面,则下列命题中为真命题的是( )
是不重合的两平面,则下列命题中为真命题的是( )
A.若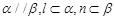 ,则 ,则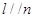 | B.若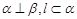 ,则 ,则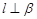 |
C.若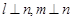 ,则 ,则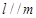 | D.若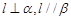 ,则 ,则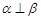 |
已知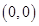 ,
,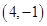 两点到直线
两点到直线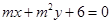 的距离相等,那么
的距离相等,那么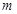 可取得不同实数值个数为( )
可取得不同实数值个数为( )
| A.1 | B.2 | C.3 | D.4 |
四面体SABC中,E,F,G分别是棱SC,AB,SB的中点,若异面直线SA与BC所成的角等于45º,则∠EGF等于( )
| A.90º | B.60º或120º | C.45º | D.45º或135º |
三条直线相交于一点,可能确定的平面有
A.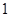 个 个 | B.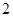 个 个 | C.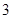 个 个 | D.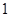 个或 个或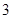 个 个 |
下列命题中,正确的是( )
| A.经过两条相交直线,有且只有一个平面 |
| B.经过一条直线和一点,有且只有一个平面 |
| C.若平面α与平面β相交,则它们只有有限个公共点 |
| D.若两个平面有三个公共点,则这两个平面重合 |
如图,在长方体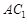 中,
中, ,
,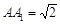 ,
,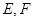 分别是面
分别是面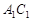 ,面
,面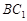 的中心,则
的中心,则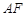 和
和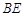 所成的角为( )
所成的角为( )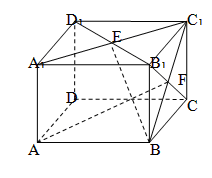
A.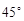 | B.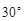 | C.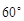 | D.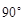 |