题目内容
从某批产品中,有放回地抽取产品二次,每次随机抽取1件,假设事件A“取出的2件产品都是二等品”的概率P(A)=0.04
(1)求从该批产品中任取1件是二等品的概率;
(2)若该批产品共10件,从中任意抽取2件;X表示取出的2件产品中二等品的件数,求X的分布列.
(1)求从该批产品中任取1件是二等品的概率;
(2)若该批产品共10件,从中任意抽取2件;X表示取出的2件产品中二等品的件数,求X的分布列.
(1) 0.2 (2) X的分布列为
| X | 0 | 1 | 2 |
| P | 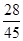 | 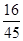 | 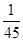 |
解:(1)设任取一件产品是二等品的概率为p,依题意有P(A)=p2=0.04,
解得p1=0.2,p2=-0.2(舍去).
故从该批产品中任取1件是二等品的概率为0.2.
(2)若该批产品共10件,由(1)知其二等品有10×0.2=2件,
故X的可能取值为0,1,2.
P(X=0)=
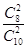 =
=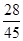 .
.P(X=1)
 =
=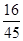 .
.P(X=2)=
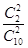 =
=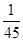 .
.所以X的分布列为
| X | 0 | 1 | 2 |
| P | 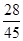 | 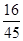 | 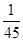 |

练习册系列答案
相关题目


 表示经销一辆汽车的利润.
表示经销一辆汽车的利润.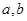 的值;
的值; :“购买该品牌汽车的3位顾客中,至多有1位采用3期付款”的概率
:“购买该品牌汽车的3位顾客中,至多有1位采用3期付款”的概率 ;(3)求
;(3)求 .
. (n=1,2,3,4),其中a是常数,则P(
(n=1,2,3,4),其中a是常数,则P( <X<
<X< )的值为( )
)的值为( )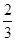



 为摸出两球中白球的个数,
为摸出两球中白球的个数,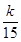 (k=1,2,3,4,5),则P
(k=1,2,3,4,5),则P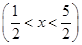 =________.
=________.