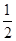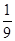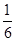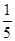题目内容
甲、乙两人玩猜数字游戏,规则如下:
①连续竞猜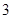 次,每次相互独立;
次,每次相互独立;
②每次竟猜时,先由甲写出一个数字,记为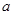 ,再由乙猜测甲写的数字,记为
,再由乙猜测甲写的数字,记为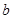 ,已知
,已知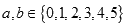 ,若
,若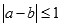 ,则本次竞猜成功;
,则本次竞猜成功;
③在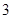 次竞猜中,至少有
次竞猜中,至少有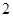 次竞猜成功,则两人获奖.
次竞猜成功,则两人获奖.
(Ⅰ) 求甲乙两人玩此游戏获奖的概率;
(Ⅱ)现从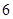 人组成的代表队中选
人组成的代表队中选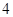 人参加此游戏,这
人参加此游戏,这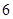 人中有且仅有
人中有且仅有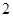 对双胞胎,记选出的
对双胞胎,记选出的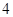 人中含有双胞胎的对数为
人中含有双胞胎的对数为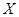 ,求
,求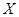 的分布列和期望.
的分布列和期望.
①连续竞猜
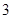 次,每次相互独立;
次,每次相互独立;②每次竟猜时,先由甲写出一个数字,记为
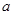 ,再由乙猜测甲写的数字,记为
,再由乙猜测甲写的数字,记为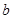 ,已知
,已知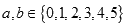 ,若
,若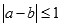 ,则本次竞猜成功;
,则本次竞猜成功;③在
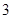 次竞猜中,至少有
次竞猜中,至少有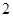 次竞猜成功,则两人获奖.
次竞猜成功,则两人获奖.(Ⅰ) 求甲乙两人玩此游戏获奖的概率;
(Ⅱ)现从
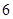 人组成的代表队中选
人组成的代表队中选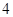 人参加此游戏,这
人参加此游戏,这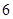 人中有且仅有
人中有且仅有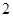 对双胞胎,记选出的
对双胞胎,记选出的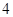 人中含有双胞胎的对数为
人中含有双胞胎的对数为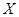 ,求
,求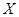 的分布列和期望.
的分布列和期望. (1)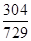
(2)分布列为
∴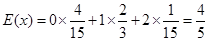
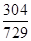
(2)分布列为
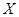 |  | 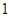 | 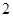 |
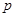 | 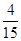 | 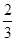 | 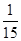 |
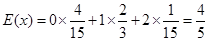
试题分析:解:(Ⅰ)记事件
 为甲乙两人一次竞猜成功,则
为甲乙两人一次竞猜成功,则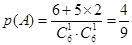
则甲乙两人获奖的概率为
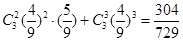
(Ⅱ)由题意可知6人中选取4人,双胞胎的对数
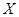 取值为0,1,2
取值为0,1,2则
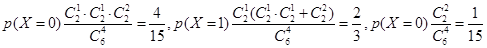 ,
, ∴分布列为
∴分布列为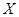 |  | 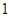 | 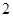 |
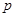 | 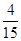 | 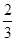 | 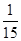 |
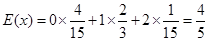
点评:主要是考查了古典概型概率和分布列的求解,属于基础题。

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目



 表示经销一辆汽车的利润.
表示经销一辆汽车的利润.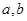 的值;
的值; :“购买该品牌汽车的3位顾客中,至多有1位采用3期付款”的概率
:“购买该品牌汽车的3位顾客中,至多有1位采用3期付款”的概率 ;(3)求
;(3)求 .
.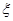 ,求
,求 名同学参加某高校的自主招生面试,已知采用抽签的方式随机确定各考生的面试顺序(序号为
名同学参加某高校的自主招生面试,已知采用抽签的方式随机确定各考生的面试顺序(序号为 ).
). ,求随机变量
,求随机变量 ,求
,求 为摸出两球中白球的个数,
为摸出两球中白球的个数, ,求
,求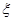 的分布列为
的分布列为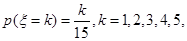 则
则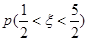 等于 ( )
等于 ( )