题目内容
若 是双曲线
是双曲线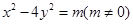 上一点,且满足
上一点,且满足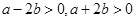 ,则该点
,则该点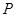 一定位于双曲线( )
一定位于双曲线( )
 是双曲线
是双曲线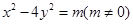 上一点,且满足
上一点,且满足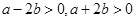 ,则该点
,则该点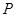 一定位于双曲线( )
一定位于双曲线( )| A.右支上 | B.上支上 | C.右支上或上支上 | D.不能确定 |
A
试题分析:由
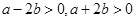 得:
得: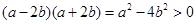 ,另把点
,另把点 代入双曲线
代入双曲线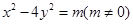 得:
得: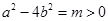 ,即有
,即有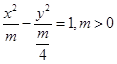 ,故双曲线焦点落在x轴上,又由
,故双曲线焦点落在x轴上,又由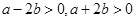 两式相加得:
两式相加得: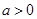 ,所以点
,所以点 一定位于双曲线右支上。故选A。
一定位于双曲线右支上。故选A。点评:要得到双曲线的性质,需要把双曲线的方程变为标准形式。

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
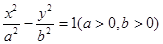 的一个焦点F引它的渐近线的垂线,垂足为M,延长FM交
的一个焦点F引它的渐近线的垂线,垂足为M,延长FM交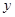 轴于E,若FM=2ME,则该双曲线的离心主经为 ( )
轴于E,若FM=2ME,则该双曲线的离心主经为 ( )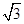
 能否作直线
能否作直线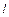 ,使
,使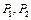 ,且点A是线段
,且点A是线段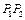 的中点?这样的直线存在吗?若存在,求出直线
的中点?这样的直线存在吗?若存在,求出直线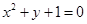 与双曲线
与双曲线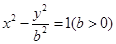 的渐近线相切,则此双曲线的焦距等于( )
的渐近线相切,则此双曲线的焦距等于( ) 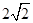
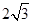
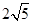
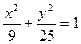 共焦点,它们的离心率之和为
共焦点,它们的离心率之和为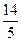 ,求双曲线方程.(10分)
,求双曲线方程.(10分) 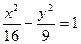 右支点上的一点P到右焦点的距离为2,则P点到左焦点的距离为
右支点上的一点P到右焦点的距离为2,则P点到左焦点的距离为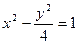 ,过点P(1,1)作直线
,过点P(1,1)作直线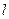 , 使
, 使 的离心率
的离心率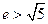 的概率是 。
的概率是 。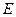 的中心在原点,焦点在坐标轴上,离心率
的中心在原点,焦点在坐标轴上,离心率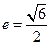 ,且双曲线过点
,且双曲线过点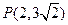 ,求双曲线
,求双曲线