题目内容
9.以直线x±2y=0为渐近线,且截直线x-y-3=0所得弦长为$\frac{8\sqrt{3}}{3}$的双曲线方程为( )| A. | $\frac{{y}^{2}}{4}$-$\frac{{x}^{2}}{8}$=1 | B. | $\frac{{x}^{2}}{8}$-$\frac{{y}^{2}}{4}$=1 | C. | y2-$\frac{{x}^{2}}{4}$=1 | D. | $\frac{{x}^{2}}{4}$-y2=1 |
分析 设双曲线方程为x2-4y2=λ,联立方程组$\left\{\begin{array}{l}{{x}^{2}-4{y}^{2}=λ}\\{x-y-3=0}\end{array}\right.$,得3x2-24x+(36+λ)=0,由椭圆弦长公式求出λ=4,由此能求出双曲线方程.
解答 解:∵双曲线以直线x±2y=0为渐近线,
∴设双曲线方程为x2-4y2=λ,
联立方程组$\left\{\begin{array}{l}{{x}^{2}-4{y}^{2}=λ}\\{x-y-3=0}\end{array}\right.$,消去y,得3x2-24x+(36+λ)=0,
设直线被双曲线截得的弦为AB,且A(x1,y1),B(x2,y2),
则${x}_{1}+{x}_{2}=8,{x}_{1}{x}_{2}=\frac{36+λ}{3}$,
△=242-432-12λ>0,
∴|AB|=$\sqrt{1+{k}^{2}}$•$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{1+1}•\sqrt{{8}^{2}-4×\frac{36+λ}{3}}$=$\frac{8\sqrt{3}}{3}$,
解得λ=4,
∴所求双曲线方程是$\frac{{x}^{2}}{4}-{y}^{2}=1$.
故选:D.
点评 本题考查双曲线标准方程的求法,是基础题,解题时要认真审题,注意椭圆性质和弦长公式的合理运用.

练习册系列答案
相关题目
14.若$\frac{2}{1-i}$=1-ai,其中a是实数,i是虚数单位,则a=( )
| A. | 1 | B. | 2 | C. | 3 | D. | -1 |
1.如果函数f(x)=$\sqrt{x+2}$+a-x存在两个不同的零点,则实数a的取值范围是( )
| A. | (-$\frac{9}{4}$,+∞) | B. | (-$\frac{9}{4}$,-2] | C. | [-2,+∞) | D. | (-$\frac{9}{4}$,0) |
18.设p:x2-5x+a<0; q:x2-4x+3<0或2${\;}^{{x}^{2}}$<26x-8
(1)当a=6时,“p∨q”为真,求x的范围
(2)¬p是¬q的充分不必要条件时,求a的取值范围.
(1)当a=6时,“p∨q”为真,求x的范围
(2)¬p是¬q的充分不必要条件时,求a的取值范围.
19.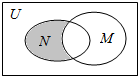 设全集U为实数集R,N={x|1<x<3},M={x|x>2},则图中阴影部分所表示的集合是( )
设全集U为实数集R,N={x|1<x<3},M={x|x>2},则图中阴影部分所表示的集合是( )
 设全集U为实数集R,N={x|1<x<3},M={x|x>2},则图中阴影部分所表示的集合是( )
设全集U为实数集R,N={x|1<x<3},M={x|x>2},则图中阴影部分所表示的集合是( )| A. | {x|x<2} | B. | {x|-2≤x≤2} | C. | {x|-2≤x<1} | D. | {x|1<x≤2} |