题目内容
【题目】设函数![]() ,已知方程
,已知方程![]() (
(![]() 为常数)在
为常数)在![]() 上恰有三个根,分别为
上恰有三个根,分别为![]() ,下述四个结论:
,下述四个结论:
①当![]() 时,
时,![]() 的取值范围是
的取值范围是![]() ;
;
②当![]() 时,
时,![]() 在
在![]() 上恰有2个极小值点和1个极大值点;
上恰有2个极小值点和1个极大值点;
③当![]() 时,
时,![]() 在
在![]() 上单调递增;
上单调递增;
④当![]() 时,
时,![]() 的取值范围为
的取值范围为![]() ,且
,且![]()
其中正确的结论个数为( )
A.1B.2C.3D.4
【答案】C
【解析】
利用三角函数的图象和性质,对每一个命题逐一分析判断得解.
①当![]() 时,
时,![]() ,令
,令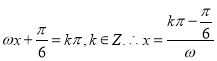 .
.
当![]() 时,
时,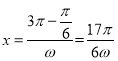 ;当
;当![]() 时,
时,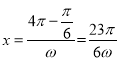 ;
;
所以![]() ,所以
,所以![]() .所以该命题是正确的;
.所以该命题是正确的;
②当![]() 时, 令
时, 令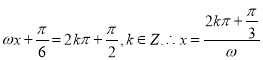 ,
,
当![]() 时,
时,![]() 令
令![]()
当![]() 时,
时,![]() 令
令![]()
因为![]() ,
,
所以![]() 在
在![]() 上有两个极大值点,所以该命题是错误的;
上有两个极大值点,所以该命题是错误的;
③当![]() 时,令
时,令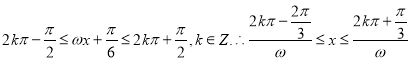 .
.
所以函数的单调递增区间为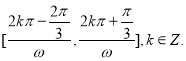
当![]() 时,
时,![]() ,
,
因为![]() ,所以
,所以![]() ,
,
因为![]() ,所以当
,所以当![]() 时,
时,![]() 在
在![]() 上单调递增.
上单调递增.
所以该命题正确;
④当![]() 时,
时,![]() ,因为
,因为![]() 所以
所以
![]() ,设
,设![]() ,如图所示,当
,如图所示,当![]() 时,直线
时,直线![]() 和函数的图象有三个交点.此时
和函数的图象有三个交点.此时![]() .
.
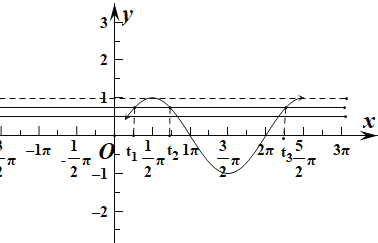
所以![]() 所以
所以![]() .所以该命题正确.
.所以该命题正确.
故选:![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目