题目内容
12.设随机变量ξ~N(μ,σ2),函数f(x)=x2+4x+ξ没有零点的概率是0.5,则μ等于( )| A. | 1 | B. | 4 | C. | 2 | D. | 不能确定 |
分析 由题中条件:“函数f(x)=x2+4x+ξ没有零点”可得ξ>4,结合正态分布的图象的对称性可得μ值.
解答 解:函数f(x)=x2+4x+ξ没有零点,
即二次方程x2+4x+ξ=0无实根得ξ>4,
∵函数f(x)=x2+4x+ξ没有零点的概率是0.5,
∴P(ξ>4)=0.5,
由正态曲线的对称性知μ=4,
故选:B.
点评 从形态上看,正态分布是一条单峰、对称呈钟形的曲线,其对称轴为x=μ,并在x=μ时取最大.

练习册系列答案
相关题目
3.集合P={x,1},Q={0,1,2},P∩Q={0,1},则x为( )
| A. | 0 | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
7.已知双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{4}$=1(a>0)的实轴长、虚轴长、焦距长成等差数列,则双曲线的渐近线方程为( )
| A. | y=$±\frac{5}{4}$x | B. | y=$±\frac{4}{5}$x | C. | y=$±\frac{3}{4}$x | D. | y=$±\frac{4}{3}$x |
4.若(m-1)+(3m+2)i是纯虚数,则实数m的值为( )
| A. | 1 | B. | 1或2 | C. | 0 | D. | -1、1、2 |
2.若函数f(x)满足f(2)=3,且f(x+3)=3f(x),则f(2015)=( )
| A. | 3670 | B. | 3671 | C. | 3672 | D. | 3673 |
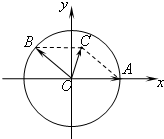 如图,在平面直角坐标系xOy上,点A(1,0),点B在单位圆上,∠AOB=θ(0<θ<π).
如图,在平面直角坐标系xOy上,点A(1,0),点B在单位圆上,∠AOB=θ(0<θ<π).