题目内容
【题目】如图,三棱柱中ABC﹣A1B1C1中,点A1在平面ABC内的射影D为棱AC的中点,侧面A1ACC1为边长为2的菱形,AC⊥CB,BC=1. 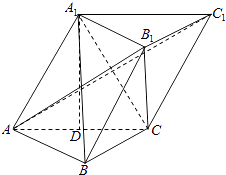
(1)证明:AC1⊥平面A1BC;
(2)求三棱锥B﹣A1B1C的体积.
【答案】
(1)证明:∵A1D⊥平面ABC,1D平面A1ACC1,
∴平面1ACC1⊥平面ABC,∵平面A1ACC1∩平面ABC=AC,CA⊥CB,CB平面ABC,
∴BC⊥平面A1ACC1,∵AC1平面A1ACC1,
∴BC⊥AC1,
∵侧面A1ACC1为菱形,∴A1C⊥AC1,
又∵A1C平面A1BC,BC平面A1BC,A1C∩BC=C,
∴AC1⊥平面A1BC,
(2)解:∵AD=1,A1A=2,∴A1D= ![]() .
.
∴ ![]() =S△ABCA1D=
=S△ABCA1D= ![]() =
= ![]() .
.
![]() =
= ![]() =
= ![]() S△ABCA1D=
S△ABCA1D= ![]() ,
,
∴ ![]() =
= ![]() ﹣
﹣ ![]() ﹣
﹣ ![]() =
= ![]() .
.
【解析】(1)由A1D⊥平面ABC得平面1ACC1⊥平面ABC,于是BC⊥平面A1ACC1 , 推出BC⊥AC1 , 由菱形的性质可知A1C⊥AC1 , 于是AC1⊥平面A1BC.(2)三棱锥B﹣A1B1C的体积等于三棱柱的体积减去两个棱锥的体积.
【考点精析】关于本题考查的直线与平面垂直的判定,需要了解一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想才能得出正确答案.

【题目】某数学兴趣小组为了研究人的脚的大小与身高的关系,随机抽测了20位同学,得到如下数据:
序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
身高 | 192 | 164 | 172 | 177 | 176 | 159 | 171 | 166 | 182 | 166 |
脚长 | 48 | 38 | 40 | 43 | 44 | 37 | 40 | 39 | 46 | 39 |
序号 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
身高 | 169 | 178 | 167 | 174 | 168 | 179 | 165 | 170 | 162 | 170 |
脚长 | 43 | 41 | 40 | 43 | 40 | 44 | 38 | 42 | 39 | 41 |
(Ⅰ)请根据“序号为5的倍数”的几组数据,求出![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(Ⅱ)若“身高大于175厘米”的为“高个”,“身高小于等于175厘米”的为“非高个”;“脚长大于42码”的为“大脚”,“脚长小于等于42码”的为“非大脚”.请根据上表数据完成![]() 列联表,并根据列联表中数据说明能有多大的把握认为脚的大小与身高之间有关系.
列联表,并根据列联表中数据说明能有多大的把握认为脚的大小与身高之间有关系.
附表及公式: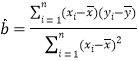 ,
,![]() ,
,![]() .
.
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() 列联表:
列联表:
高个 | 非高个 | 总计 | |
大脚 | |||
非大脚 | |||
总计 |