题目内容
【题目】已知函数
．
（Ⅰ）求函数
的最小正周期；
（Ⅱ）求函数在区间
上的最值以及相应的x的取值．
【答案】（Ⅰ）
；（Ⅱ）
时，
取得最大值2；
时，取得最小值
.
【解析】
（Ⅰ）利用二倍角和两角和与差以及辅助角公式将函数化为y＝Asin（ωx+φ）的形式，利用三角函数的周期公式求函数的最小正周期．
（Ⅱ）利用x∈[
，
]上时，求出内层函数的取值范围，结合三角函数的图象和性质，求出f（x）的最大值和最小值．
(Ⅰ)因为函数f（x）＝4cosxsin（x
）
1．
化简可得：f（x）＝4cosxsinxcos
4cos2xsin
1
sin2x+2cos2x1sin2x+cos2x＝2sin（2x）
所以的最小正周期为
．
(Ⅱ)因为
，所以
．
当
，即
时，f（x）取得最大值2；
当
，即时，f（x）取得最小值-1．
练习册系列答案
相关题目
【题目】如图，在三棱锥S﹣ABC中，平面SAB⊥平面SBC，AB⊥BC，AS=AB，过A作AF⊥SB，垂足为F，点E，G分别是棱SA，SC的中点．求证：
（1）平面EFG∥平面ABC；
（2）BC⊥SA．
【题目】（ 2013湖南）某人在如图所示的直角边长为4米的三角形地块的每个格点（指纵、横直线的交叉点以及三角形顶点）处都种了一株相同品种的作物．根据历年的种植经验，一株该种作物的年收获Y（单位：kg）与它的“相近”作物株数X之间的关系如下表所示：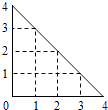 
X | 1 | 2 | 3 | 4 |
Y | 51 | 48 | 45 | 42 |
这里，两株作物“相近”是指它们之间的直线距离不超过1米．
（1）从三角形地块的内部和边界上分别随机选取一株作物，求它们恰 好“相近”的概率；
（2）在所种作物中随机选取一株，求它的年收获量的分布列与数学期望．
