题目内容
已知直线l1∥l2，A是l1，l2之间的一定点，并且A点到l1，l2的距离分别为3和4，B是直线l2上一动点，作AC⊥AB，且使AC与直线l1交于点C，则△ABC面积的最小值为（ ）
分析：过A作l1、l2的垂线，分别交l1、l2于E、F．由直角三角形中三角函数的定义，算出AC=
且AB=
，从而得到△ABC面积S=
AB•AC=
，利用正弦函数的有界性，可得θ=
时△ABC面积有最小值12．
| 3 |
| cosθ |
| 4 |
| sinθ |
| 1 |
| 2 |
| 12 |
| sin2θ |
| π |
| 4 |
解答：解：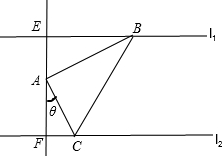
过A作l1、l2的垂线，分别交l1、l2于E、F
则AE=3，AF=4
设∠FAC=θ，则Rt△ACF中，AC=
=
Rt△ABE中，∠ABE=θ
可得AB=
=
∴△ABC面积为S=
AB•AC=
=
∵θ∈（0，
）
∴当且仅当θ=
时，sin2θ=1达到最大值1，
此时△ABC面积有最小值12
故选：B
过A作l1、l2的垂线，分别交l1、l2于E、F则AE=3，AF=4
设∠FAC=θ，则Rt△ACF中，AC=
| AF |
| cosθ |
| 3 |
| cosθ |
Rt△ABE中，∠ABE=θ
可得AB=
| AE |
| sinθ |
| 4 |
| sinθ |
∴△ABC面积为S=
| 1 |
| 2 |
| 6 |
| sinθcosθ |
| 12 |
| sin2θ |
∵θ∈（0，
| π |
| 2 |
∴当且仅当θ=
| π |
| 4 |
此时△ABC面积有最小值12
故选：B
点评：此题考查了直角三角形中锐角三角函数定义，正弦函数的定义域及值域及二倍角的正弦函数公式，利用了数形结合的思想，属于中档题．
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
相关题目
如图示，已知直线l1∥l2，点A是l1，l2之间的一个定点，且A到l1，l2的距离分别为4、3，点B是直线l1上的动点，若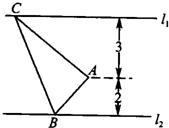
如图，已知直线l1∥l2，点A是l1，l2之间的定点，点A到l1，l2之间的距离分别为3和2，点B是l2上的一动点，作AC⊥AB，且AC与l1交于点C，则△ABC的面积的最小值为
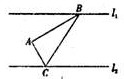如图，已知直线l1∥l2，点A是l1，l2上两直线之间的动点，且到l1距离为4，到l2距离为3，若
α，l2∩α=A,则l1,l2为异面直线