题目内容
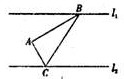 如图,已知直线l1∥l2,点A是l1,l2上两直线之间的动点,且到l1距离为4,到l2距离为3,若
如图,已知直线l1∥l2,点A是l1,l2上两直线之间的动点,且到l1距离为4,到l2距离为3,若| AC |
| AB |
分析:过A作直线l1的垂线交点分别为E和F,由l1∥l2,得到直线EF也与l2垂直,从而得到AE及AF的值,由两向量的数量积积为0得到两向量垂直,即AB与AC垂直,设∠FAC=θ,则有∠EAB=
-θ,分别在直角三角形AEB和AFC中,由AE,AF,及设出的角度利用余弦函数定义表示出AB积AC,由三角形ABC为直角三角形,用直角边AB与AC的乘积表示出三角形的面积,利用诱导公式及二倍角的正弦函数公式化简后,根据正弦函数的值域即可得到面积的最小值.
| π |
| 2 |
解答: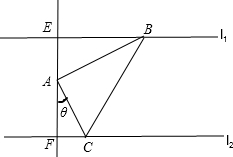
解:过A作l1的垂线,与l1,l2分别交于点E和F,又l1∥l2,故直线EF也与l2垂直,
则根据题意得AE=4,AF=3,
∵
•
=0,∴AB⊥AC,即∠BAC=
,
令∠FAC=θ,则∠EAB=
-θ,
∴cosθ=
,则AC=
,
同理可得AB=
,
∴S△ABC=
AB•AC=
=
=
≥12,
则△ABC的面积最小值为12.
故选C

解:过A作l1的垂线,与l1,l2分别交于点E和F,又l1∥l2,故直线EF也与l2垂直,
则根据题意得AE=4,AF=3,
∵
| AC |
| AB |
| π |
| 2 |
令∠FAC=θ,则∠EAB=
| π |
| 2 |
∴cosθ=
| 3 |
| AC |
| 3 |
| cosθ |
同理可得AB=
| 4 | ||
cos(
|
∴S△ABC=
| 1 |
| 2 |
| 6 | ||
cosθcos(
|
| 12 |
| 2sinθcosθ |
| 12 |
| sin2θ |
则△ABC的面积最小值为12.
故选C
点评:此题考查了平面向量数量积的运算,锐角三角函数定义,正弦函数的定义域及值域,诱导公式及二倍角的正弦函数公式,利用了数形结合的思想,过A作出已知直线的垂线EF是解本题的关键.

练习册系列答案
相关题目
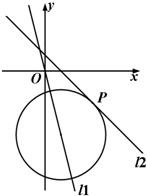 如图,已知直线l1:4x+y=0,直线l2:x+y-1=0以及l2上一点P(3,-2).
如图,已知直线l1:4x+y=0,直线l2:x+y-1=0以及l2上一点P(3,-2).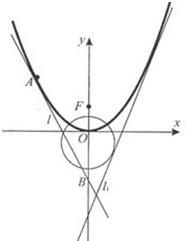 如图,已知直线l1:y=2x+m(m<0)与抛物线C1:y=ax2(a>0)和圆C2:x2+(y+1)2=5都相切,F是C1的焦点.
如图,已知直线l1:y=2x+m(m<0)与抛物线C1:y=ax2(a>0)和圆C2:x2+(y+1)2=5都相切,F是C1的焦点. 如图,已知直线l1:4x+y=0,直线l2:x+y-1=0以及l2上一点P(3,-2).求有圆心在l1上且与直线l2相切于点P的圆的方程.
如图,已知直线l1:4x+y=0,直线l2:x+y-1=0以及l2上一点P(3,-2).求有圆心在l1上且与直线l2相切于点P的圆的方程.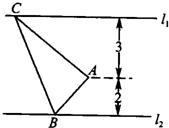 如图,已知直线l1∥l2,点A是l1,l2之间的定点,点A到l1,l2之间的距离分别为3和2,点B是l2上的一动点,作AC⊥AB,且AC与l1交于点C,则△ABC的面积的最小值为
如图,已知直线l1∥l2,点A是l1,l2之间的定点,点A到l1,l2之间的距离分别为3和2,点B是l2上的一动点,作AC⊥AB,且AC与l1交于点C,则△ABC的面积的最小值为