题目内容
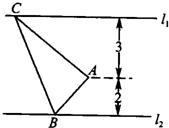如图，已知直线l1∥l2，点A是l1，l2之间的定点，点A到l1，l2之间的距离分别为3和2，点B是l2上的一动点，作AC⊥AB，且AC与l1交于点C，则△ABC的面积的最小值为6
6
．分析：用θ表示∠ABM，如图，通过解RT△ABM，RT△ABM 表示出AB，AC，利用S=
AB•AC将S表示为关于θ的三角函数，利用三角函数性质求出最值．
| 1 |
| 2 |
解答：
解：过A作l1，l2之间的垂线，垂足分别为M，N．设∠ABM=θ（0＜θ＜
）
在RT△ABM中，sinθ=
=
，AB=
在RT△ABM中，∠CAN=∠ABM=θ
=
=
，AC=
△ABC的面积S=
AB•AC=
=
当2θ=90°，即θ=45°时，S取得最小值6
故答案为：6
解：过A作l1，l2之间的垂线，垂足分别为M，N．设∠ABM=θ（0＜θ＜| π |
| 2 |
在RT△ABM中，sinθ=
| AM |
| AB |
| 2 |
| AB |
| 2 |
| sinθ |
在RT△ABM中，∠CAN=∠ABM=θ
| 3 |
| cosθ |
| AN |
| AC |
| 3 |
| AC |
| 3 |
| cosθ |
△ABC的面积S=
| 1 |
| 2 |
| 6 |
| 2sinθ•cosθ |
| 6 |
| sin2θ |
当2θ=90°，即θ=45°时，S取得最小值6
故答案为：6
点评：本题考查解三角形知识，函数思想、建模解模．考查分析、解决、计算能力．
练习册系列答案
相关题目
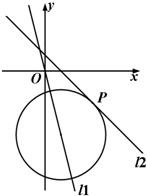如图，已知直线l1：4x+y=0，直线l2：x+y-1=0以及l2上一点P（3，-2）．
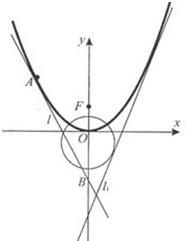如图，已知直线l1：y=2x+m（m＜0）与抛物线C1：y=ax2（a＞0）和圆C2：x2+（y+1）2=5都相切，F是C1的焦点．
如图，已知直线l1：4x+y=0，直线l2：x+y-1=0以及l2上一点P（3，-2）．求有圆心在l1上且与直线l2相切于点P的圆的方程．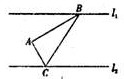
如图，已知直线l1∥l2，点A是l1，l2上两直线之间的动点，且到l1距离为4，到l2距离为3，若