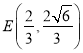题目内容
【题目】已知抛物线![]()
![]() 的焦点为
的焦点为![]() ,过抛物线
,过抛物线![]() 上的动点
上的动点![]() (除顶点
(除顶点![]() 外)作
外)作![]() 的切线
的切线![]() 交
交![]() 轴于点
轴于点![]() .过点
.过点![]() 作直线
作直线![]() 的垂线
的垂线![]() (垂足为
(垂足为![]() )与直线
)与直线![]() 交于点
交于点![]() .
.
(Ⅰ)求焦点![]() 的坐标;
的坐标;
(Ⅱ)求证:![]() ;
;
(Ⅲ)求线段![]() 的长.
的长.
【答案】(Ⅰ)![]() (Ⅱ)见解析(Ⅲ)
(Ⅱ)见解析(Ⅲ)![]() .
.
【解析】试题分析:(Ⅰ)由抛物线方程![]() ,可得
,可得![]() ,从而得焦点
,从而得焦点![]() 的坐标;(Ⅱ)设
的坐标;(Ⅱ)设![]() ,利用导数的几何意义可得过点
,利用导数的几何意义可得过点![]() 的切线
的切线![]() 的斜率为
的斜率为![]() ,从而得
,从而得![]() ,根据过两点的斜率公式可得
,根据过两点的斜率公式可得![]() ,从而可得结论;(Ⅲ)由(Ⅱ)可设直线
,从而可得结论;(Ⅲ)由(Ⅱ)可设直线![]() 的方程为
的方程为![]() ,
,![]() .直线
.直线![]() 的方程为
的方程为![]()
![]() .设
.设![]() 和
和![]() 交点
交点![]() 的坐标为
的坐标为![]() ,联立直线方程可得
,联立直线方程可得![]() ,
,![]() ,代入圆的方程结果.
,代入圆的方程结果.
试题解析:(Ⅰ)由抛物线方程![]() ,可得
,可得![]() ,可得
,可得 ![]()
(Ⅱ)设![]() .由
.由![]() ,得
,得![]() ,则过点
,则过点![]() 的切线
的切线![]() 的斜率为
的斜率为![]() .
.
则过点![]() 的切线
的切线![]() 方程为
方程为![]() .令
.令![]() ,得
,得![]() ,即
,即![]() .又点
.又点![]() 为抛物线上除顶点
为抛物线上除顶点![]() 外的动点,
外的动点,![]() ,则
,则![]() .而由已知得
.而由已知得![]() ,则
,则![]() .又
.又![]() ,即
,即![]() 与
与![]() 不重合,即
不重合,即![]() .
.
(Ⅲ)由(Ⅱ)问,直线![]() 的方程为
的方程为![]() ,
,![]() .直线
.直线![]() 的方程为
的方程为![]()
![]() .设
.设![]() 和
和![]() 交点
交点![]() 的坐标为
的坐标为![]() 则
则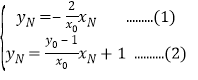
由(1)式得,![]() (由于
(由于![]() 不与原点重合,故
不与原点重合,故![]() ).代入(2),化简得
).代入(2),化简得![]()
![]() .又
.又![]() ,化简得,
,化简得,![]() (
(![]() ).
).
即点![]() 在以
在以![]() 为圆心,1为半径的圆上.(原点与
为圆心,1为半径的圆上.(原点与![]() 除外)
除外)
即![]() .
.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目