题目内容
【题目】如图，半圆O的直径AB=2，点C在AB的延长线上，BC=1，点P为半圆上异于A，B两点的一个动点，以点P为直角顶点作等腰直角
，且点D与圆心O分布在PC的两侧，设
．
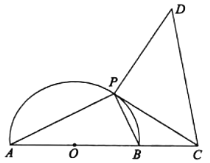
（1）把线段PC的长表示为
的函数；
（2）求四边形ACDP面积的最大值．
【答案】（1）
， 
； （2）5
【解析】
（1）根据图形，解三角形，利用余弦定理，将线段PC的长表示为
的函数；
（2）将四边形ACDP面积表示为角的函数,再利用三角函数求最值.
解：（1）依题设易知
是以
为直角的直角三角形，
又
，所以
.
在
，由余弦定理得，
.
所以， 定义域为.
（2）四边形ACDP面积为
，
则
其中
为锐角.
因为
所以
.
又因为
，所以
，
所以当
时，取得最大值为
.
所以四边形ACDP面积的最大值为5 .
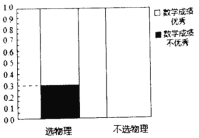
【题目】某省即将实行新高考，不再实行文理分科.某校为了研究数学成绩优秀是否对选择物理有影响，对该校2018级的1000名学生进行调查，收集到相关数据如下：
（1）根据以上提供的信息，完成
列联表，并完善等高条形图；
选物理 | 不选物理 | 总计 | |
数学成绩优秀 | |||
数学成绩不优秀 | 260 | ||
总计 | 600 | 1000 |
（2）能否在犯错误的概率不超过0.05的前提下认为数学成绩优秀与选物理有关？
附：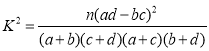
临界值表：
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
【题目】一饮料店制作了一款新饮料，为了进行合理定价先进行试销售，其单价
（元）与销量
（杯）的相关数据如下表：
单价 | 8.5 | 9 | 9.5 | 10 | 10.5 |
销量 | 120 | 110 | 90 | 70 | 60 |
（1）已知销量与单价具有线性相关关系，求关于的线性回归方程；
（2）若该款新饮料每杯的成本为8元，试销售结束后，请利用（1）所求的线性回归方程确定单价定为多少元时，销售的利润最大？（结果四舍五入保留到整数）
附：线性回归方程
中斜率和截距最小二乗法估计计算公式：
，
，
，
.
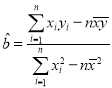【题目】“黄梅时节家家雨”“梅雨如烟暝村树”“梅雨暂收斜照明”……江南梅雨的点点滴滴都流润着浓烈的诗情.每年六、七月份，我国长江中下游地区进入持续25天左右的梅雨季节，如图是江南
镇2009～2018年梅雨季节的降雨量（单位：
）的频率分布直方图，试用样本频率估计总体概率，解答下列问题：
“梅实初黄暮雨深”.请用样本平均数估计镇明年梅雨季节的降雨量；
“江南梅雨无限愁”.镇的杨梅种植户老李也在犯愁，他过去种植的甲品种杨梅，他过去种植的甲品种杨梅，亩产量受降雨量的影响较大（把握超过八成）.而乙品种杨梅2009～2018年的亩产量（
/亩）与降雨量的发生频数（年）如
列联表所示（部分数据缺失）.请你帮助老李排解忧愁，他来年应该种植哪个品种的杨梅受降雨量影响更小？
（完善列联表，并说明理由）.
亩产量\降雨量 |
|
| 合计 |
<600 | 2 | ||
| 1 | ||
合计 | 10 |
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.703 |
（参考公式：
，其中
）
