题目内容
（2013•淄博二模）已知抛物线y2=4x的焦点为F2，点F1与F2关于坐标原点对称，直线m垂直于x轴（垂足为T），与抛物线交于不同的两点P、Q且
•
=-5．
（I）求点T的横坐标x0；
（II）若以F1，F2为焦点的椭圆C过点(1，
)．
①求椭圆C的标准方程；
②过点F2作直线l与椭圆C交于A，B两点，设
=λ
，若λ∈[-2，-1]，求|
+
|的取值范围．
| F1P |
| F2Q |
（I）求点T的横坐标x0；
（II）若以F1，F2为焦点的椭圆C过点(1，
| ||
| 2 |
①求椭圆C的标准方程；
②过点F2作直线l与椭圆C交于A，B两点，设
| F2A |
| F2B |
| TA |
| TB |
分析：（Ⅰ）由题意得到F1和F2的坐标，设出P，Q的坐标，然后直接利用
•
=-5进行求解；
（Ⅱ）①设出椭圆标准方程，利用椭圆过点(1，
)，结合a2=b2+1 即可求得a2，b2的值，则椭圆方程可求；
②当直线斜率不存在时，直接求解A，B的坐标得到|
+
|的值，当直线斜率存在时，设出直线方程，和椭圆方程联立后，利用
=λ
，消掉点的坐标得到λ与k的关系，根据λ的范围求k的范围，然后把|
+
|转化为含有k的函数式，最后利用基本不等式求出|
+
|的取值范围．
| F1P |
| F2Q |
（Ⅱ）①设出椭圆标准方程，利用椭圆过点(1，
| ||
| 2 |
②当直线斜率不存在时，直接求解A，B的坐标得到|
| TA |
| TB |
| F2A |
| F2B |
| TA |
| TB |
| TA |
| TB |
解答：解：（Ⅰ）如图，
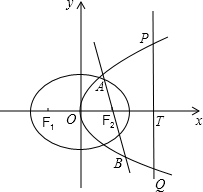
由题意得F2（1，0），F1（-1，0），设P（x0，y0），则Q（x0，-y0），
则
=(x0+1，y0)，
=(x0-1，-y0)．
由
•
=-5，
得x02-1-y02=-5，即x02-y02=-4 ①
又P（x0，y0）在抛物线上，则y02=4x0 ②
联立①、②得，x02-4x0+4=0，解得：x0=2．
所以点T的横坐标x0=2．
（Ⅱ）（ⅰ）设椭圆的半焦距为c，由题意得c=1，
设椭圆C的标准方程为
+
=1(a＞b＞0)，
因椭圆C过点(1，
)，
则
+
=1 ③
又a2=b2+1 ④
将④代入③，解得b2=1或b2=-
（舍去）
所以a2=b2+1=2．
故椭圆C的标准方程为
+y2=1．
（ⅱ）1）当直线l的斜率不存在时，即λ=-1时，A(1，
)，B(1，-
)，
又T（2，0），所以|
+
|=|(-1，
)+(-1，-
)|=2；
2）当直线l的斜率存在时，即λ∈[-2，-1）时，设直线l的方程为y=k（x-1）．
由
，得（1+2k2）x2-4k2x+2k2-2=0
设A（x1，y1），B（x2，y2），显然y1≠0，y2≠0，则由根与系数的关系，
可得：x1+x2=
，x1•x2=
．
y1+y2=k(x1+x2)-2k=
⑤
y1•y2=k2(x1x2-(x1+x2)+1)=
⑥
因为
=λ
，所以
=λ，且λ＜0．
将⑤式平方除以⑥式得：λ+
+2=
由λ∈[-2，-1），得λ+
∈[-
，-2)，即λ+
+2∈[-
，0)．
故-
≤
＜0，解得k2≥
．
因为
=(x1-2，y1)，
=(x2-2，y2)，所以
+
=(x1+x2-4，y1+y2)，
又x1+x2-4=
，
故|
+
|2=(x1+x2-4)2+(y1+y2)2=
+
=
=4+
+
．
令t=
，因为k2≥
，所以0＜
≤
，即t∈(0，
]，
所以|
+
|2=2t2+10t+4=2(t+
)2-
∈(4，
]．
所以|
+
|∈(2，
]
综上所述：|
+
|∈[2，
]．
由题意得F2（1，0），F1（-1，0），设P（x0，y0），则Q（x0，-y0），
则
| F1P |
| F2Q |
由
| F1P |
| F2Q |
得x02-1-y02=-5，即x02-y02=-4 ①
又P（x0，y0）在抛物线上，则y02=4x0 ②
联立①、②得，x02-4x0+4=0，解得：x0=2．
所以点T的横坐标x0=2．
（Ⅱ）（ⅰ）设椭圆的半焦距为c，由题意得c=1，
设椭圆C的标准方程为
| x2 |
| a2 |
| y2 |
| b2 |
因椭圆C过点(1，
| ||
| 2 |
则
| 1 |
| a2 |
| ||
| b2 |
又a2=b2+1 ④
将④代入③，解得b2=1或b2=-
| 1 |
| 2 |
所以a2=b2+1=2．
故椭圆C的标准方程为
| x2 |
| 2 |
（ⅱ）1）当直线l的斜率不存在时，即λ=-1时，A(1，
| ||
| 2 |
| ||
| 2 |
又T（2，0），所以|
| TA |
| TB |
| ||
| 2 |
| ||
| 2 |
2）当直线l的斜率存在时，即λ∈[-2，-1）时，设直线l的方程为y=k（x-1）．
由
|
设A（x1，y1），B（x2，y2），显然y1≠0，y2≠0，则由根与系数的关系，
可得：x1+x2=
| 4k2 |
| 1+2k2 |
| 2k2-2 |
| 1+2k2 |
y1+y2=k(x1+x2)-2k=
| -2k |
| 1+2k2 |
y1•y2=k2(x1x2-(x1+x2)+1)=
| -k2 |
| 1+2k2 |
因为
| F2A |
| F2B |
| y1 |
| y2 |
将⑤式平方除以⑥式得：λ+
| 1 |
| λ |
| -4 |
| 1+2k2 |
由λ∈[-2，-1），得λ+
| 1 |
| λ |
| 5 |
| 2 |
| 1 |
| λ |
| 1 |
| 2 |
故-
| 1 |
| 2 |
| -4 |
| 1+2k2 |
| 7 |
| 2 |
因为
| TA |
| TB |
| TA |
| TB |
又x1+x2-4=
| -4(1+k2) |
| 1+2k2 |
故|
| TA |
| TB |
| 16(1+k2)2 |
| (1+2k2)2 |
| 4k2 |
| (1+2k2)2 |
=
| 4(1+2k2)2+10(1+2k2)+2 |
| (1+2k2)2 |
| 10 |
| 1+2k2 |
| 2 |
| (1+2k2)2 |
令t=
| 1 |
| 1+2k2 |
| 7 |
| 2 |
| 1 |
| 1+2k2 |
| 1 |
| 8 |
| 1 |
| 8 |
所以|
| TA |
| TB |
| 5 |
| 2 |
| 17 |
| 2 |
| 169 |
| 32 |
所以|
| TA |
| TB |
13
| ||
| 8 |
综上所述：|
| TA |
| TB |
13
| ||
| 8 |
点评：本题考查了椭圆的标准方程，考查了直线与圆锥曲线的关系，训练了平面向量数量积的运算，考查了分类讨论的数学解题思想，训练了利用基本不等式求最值，考查了学生的计算能力，是难度较大的题目．
练习册系列答案
同步奥数系列答案
相关题目
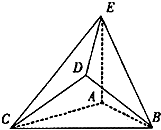（2013•淄博二模）在如图所示的几何体中，△ABC是边长为2的正三角形，AE=1，AE⊥平面ABC，平面BCD⊥平面ABC，BD=CD，且BD⊥CD．
（2013•淄博二模）如图，平行四边形ABCD中，AB=2，AD=1，∠A=60°，点M在AB边上，且AM=