题目内容
设p:?x∈(1,
)使函数g(x)=log2(tx2+2x-2)有意义,若?p为假命题,则t的取值范围为
| 5 |
| 2 |
t>-
| 1 |
| 2 |
t>-
.| 1 |
| 2 |
分析:由命题p为真命题,知存在x∈(1,
)使对数式的真数大于0成立,然后采用分离变量的办法把t分离出来,求出分离变量后的函数的值域,则t的范围可求.
| 5 |
| 2 |
解答:解:若¬P为假命题,则p为真命题.不等式tx2+2x-2>0有属于(1,
)的解,即t>
-
有属于(1,
)的解,
又1<x<
时,
<
<1,所以
-
=2(
-
)2-
∈[-
,0).
故t>-
.
故答案为t>-
.
| 5 |
| 2 |
| 2 |
| x2 |
| 2 |
| x |
| 5 |
| 2 |
又1<x<
| 5 |
| 2 |
| 2 |
| 5 |
| 1 |
| x |
| 2 |
| x2 |
| 2 |
| x |
| 1 |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故t>-
| 1 |
| 2 |
故答案为t>-
| 1 |
| 2 |
点评:本题考查了命题的否定,训练了分离变量法求字母的范围,一个命题与它的否命题真假相反,是中档题.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
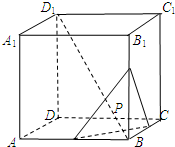 如图,正方体ABCD-A1B1C1D1的棱长为2
如图,正方体ABCD-A1B1C1D1的棱长为2