题目内容
已知⊙C的圆心在x轴上,直线y=x截⊙C所得弦长为2,且⊙C过点(2,
).
(1)求⊙C方程;
(2)设P(x,y)为⊙C上任一点,求(x-1)2+(y+3)2的最大值.
| 5 |
(1)求⊙C方程;
(2)设P(x,y)为⊙C上任一点,求(x-1)2+(y+3)2的最大值.
分析:(1)利用直线y=x截⊙C所得弦长为2,且⊙C过点(2,
),求出圆心坐标与半径,从而可求⊙C方程;
(2)利用圆的参数方程,设出点的坐标,即可求(x-1)2+(y+3)2的最大值.
| 5 |
(2)利用圆的参数方程,设出点的坐标,即可求(x-1)2+(y+3)2的最大值.
解答:解:(1)设圆心(a,0),则
∵直线y=x截⊙C所得弦长为2,且⊙C过点(2,
)
∴(
)2+12=(a-2)2+5,解得a=4,
∴所求圆的方程为(x-4)2+y2=9
(2)设
,故(x-1)2+(y+3)2=(3+3cosθ)2+(3sinθ+3)2
=9(3+2sinθ+2cosθ)=9[3+2
sin(θ+
)]≤27+18
∴(x-1)2+(y+3)2的最大值为27+18
.
∵直线y=x截⊙C所得弦长为2,且⊙C过点(2,
| 5 |
∴(
| |a| | ||
|
∴所求圆的方程为(x-4)2+y2=9
(2)设
|
=9(3+2sinθ+2cosθ)=9[3+2
| 2 |
| π |
| 4 |
| 2 |
∴(x-1)2+(y+3)2的最大值为27+18
| 2 |
点评:本题考查直线与圆的位置关系,考查圆的标准方程,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案
相关题目
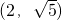 .
.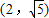 .
.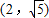 .
.