Question

（08年岳阳一中二模理）（12分） 已知梯形中，∥，，， 、分别是、上的点，∥，，是的中点，沿将 梯形翻折，使平面平面(如图)。

  （1）当时，求证：；

  （2）若以F、B、C、D为顶点的三棱锥的体积记为，求的最大值；当取得最大值时，求二面角D-BF-C的大小。

 

 

         

Answer 1

解析：∵平面平面,AE⊥EF,∴AE⊥面平面,AE⊥EF,AE⊥BE,又BE⊥EF,故可建立空间坐标系E-xyz。则A（0，0，2），B（2，0，0），G（2，2，0），

D（0，2，2），E（0，0，0）

（1）（－2，2，2）（2，2，0）

（－2，2，2）（2，2，0）＝0，∴……4分；

（2）∵AD∥面BFC，V_A-BFC＝＝4(4-x)x

即时有最大值为…………8分

（3）设平面DBF的法向量为，∵AE=2, B（2，0，0），D（0，2，2），

F（0，3，0）,∴（－2，2，2）,

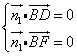则 ，即，

取x＝3，则y＝2，z＝1，∴

面BCF的一个法向量为

则cos<>= 

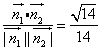
二面角D-BF-C的平面角为π-arccos…………12分