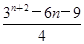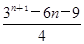题目内容
设Sn为数列{an}的前n项和,Sn=(-1)nan- ,n∈N*,则S1+S2+S3+…+S100=________.
,n∈N*,则S1+S2+S3+…+S100=________.
 ,n∈N*,则S1+S2+S3+…+S100=________.
,n∈N*,则S1+S2+S3+…+S100=________.
当n≥2时,an=Sn-Sn-1,
∴Sn=(-1)n(Sn-Sn-1)- ,
,
当n为偶数时,Sn-1=- ,
,
当n为奇数时,Sn= Sn-1-
Sn-1- ,有-
,有- =
= Sn-1-
Sn-1- ,
,
∴n为奇数时,Sn-1=0.
故S1+S2+S3+…+S100=S1+S3+S5+…+S99
=- =
= .
.
∴Sn=(-1)n(Sn-Sn-1)-
 ,
,当n为偶数时,Sn-1=-
 ,
,当n为奇数时,Sn=
 Sn-1-
Sn-1- ,有-
,有- =
= Sn-1-
Sn-1- ,
,∴n为奇数时,Sn-1=0.
故S1+S2+S3+…+S100=S1+S3+S5+…+S99
=-
 =
= .
.
练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
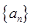 的前n项和
的前n项和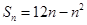
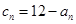 ,求数列
,求数列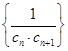 的前
的前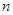 项和
项和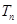
 满足:
满足: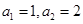 ,且
,且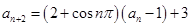 ,
, .
. ;
;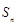
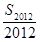 的值为________.
的值为________.