题目内容
2.已知函数f(x)=Asin(ωx+$\frac{π}{4}$)(A>0,ω>0),g(x)=tanx,它们的最小正周期之积为2π2,f(x)的最大值为2g($\frac{17π}{4}$)(1)求f(x)的单调递增区间
(2)设h(x)=$\frac{3}{2}$f2(x)+2$\sqrt{3}$cos2x,当x∈[a,$\frac{π}{3}$]时,h(x)有最小值为3,求a的值.
分析 (1)首先,根据已知条件,建立周期关系式,得到相应的ω和A的值;
(2)结合(1),利用降幂公式和辅助角公式,化简函数解析式,然后,根据正弦函数的单调性确定a的值.
解答 解:(1)∵g(x)=tanx的周期为π,
∵它们的最小正周期之积为2π2,
∴函数f(x)=Asin(ωx+$\frac{π}{4}$)的周期为2π,
∴$\frac{2π}{ω}$=2π,∴ω=1,
∵2g($\frac{17π}{4}$)=2tan(4π+$\frac{π}{4}$)=2tan$\frac{π}{4}$=2,
∴f(x)的最大值为2,
∴A=2,
∴函数f(x)=2sin(x+$\frac{π}{4}$),
令-$\frac{π}{2}$+2kπ≤x+$\frac{π}{4}$≤$\frac{π}{2}$+2kπ,k∈Z,
∴-$\frac{3π}{4}$+2kπ≤x≤$\frac{π}{4}$+2kπ,
∴f(x)的单调递增区间:[-$\frac{3π}{4}$+2kπ,$\frac{π}{4}$+2kπ],(k∈Z),
(2)结合(1),得
h(x)=$\frac{3}{2}$×4×sin2(x+$\frac{π}{4}$)+2$\sqrt{3}$cos2x,
=6×$\frac{1-cos(2x+\frac{π}{2})}{2}$+2$\sqrt{3}$×$\frac{1+cos2x}{2}$,
=3(1+sin2x)+$\sqrt{3}$cos2x+$\sqrt{3}$,
=3sin2x+$\sqrt{3}$cos2x+3+$\sqrt{3}$,
=2$\sqrt{3}$sin(2x+$\frac{π}{6}$)+3+$\sqrt{3}$,
∵x∈[a,$\frac{π}{3}$],h(x)有最小值为3,
∴sin(2x+$\frac{π}{6}$)=-$\frac{1}{2}$,
∴x=kπ-$\frac{π}{6}$,
∵当-$\frac{π}{3}$≤x≤$\frac{π}{6}$时,h(x)为单调递增,
当$\frac{π}{6}$≤x≤$\frac{2π}{3}$时,h(x)为单调递减,
∴h(x)在x=-$\frac{π}{6}$时,有最小值3,
∴a=-$\frac{π}{6}$.
点评 本题重点考查了三角函数的周期性和单调性、三角函数的最值、辅助角公式等知识,属于中档题.

 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案| A. | -1 | B. | 3 | C. | 2015 | D. | -4028 |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
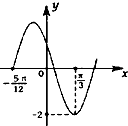 已知函数f(x)=Acos(ωx+φ)(x∈R)的图象的一部分如图所示,其中A>0,ω>0,|φ|<$\frac{π}{2}$,为了得到函数f(x)的图象,只要将函数g(x)=2cos2$\frac{x}{2}-2{sin^2}\frac{x}{2}$(x∈R)图象上所有的点( )
已知函数f(x)=Acos(ωx+φ)(x∈R)的图象的一部分如图所示,其中A>0,ω>0,|φ|<$\frac{π}{2}$,为了得到函数f(x)的图象,只要将函数g(x)=2cos2$\frac{x}{2}-2{sin^2}\frac{x}{2}$(x∈R)图象上所有的点( )| A. | 向右平移$\frac{π}{6}$个单位长度,再把所得各点的横坐标变为原来的$\frac{1}{2}$倍,纵坐标不变 | |
| B. | 向右平移$\frac{π}{6}$个单位长度,再把所得各点的横坐标变为原来的2倍;纵坐标不变 | |
| C. | 向左平移$\frac{π}{3}$个单位长度,再把得所各点的横坐标变为原来的$\frac{1}{2}$倍;纵坐标不变 | |
| D. | 向左平移$\frac{π}{3}$个单位长度,再把所得各点的横坐标变为原来的2倍,纵坐标不变 |
| A. | 有最大值,最大值为$\sqrt{3}$+1 | B. | 对称轴方程是x=$\frac{7π}{12}$+kπ,k∈Z | ||
| C. | 在区间[$\frac{π}{12}$,$\frac{7π}{12}$]上单调递增 | D. | 是周期函数,周期T=$\frac{π}{2}$ |
| A. | (2,5) | B. | (-2,-5) | C. | (-5,2) | D. | (-2,5) |