题目内容
某体育馆拟用运动场的边角地建一个矩形的健身室.如图所示,ABCD是一块边长为50 m的正方形地皮,扇形CEF是运动场的一部分,其半径为40 m,矩形AGHM就是拟建的健身室,其中G、M分别在AB和AD上,H在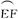 上.设矩形AGHM的面积为S,∠HCF=θ,请将S表示为θ的函数,并指出当点H在
上.设矩形AGHM的面积为S,∠HCF=θ,请将S表示为θ的函数,并指出当点H在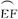 的何处时,该健身室的面积最大,最大面积是多少?
的何处时,该健身室的面积最大,最大面积是多少?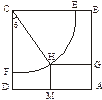
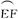 上.设矩形AGHM的面积为S,∠HCF=θ,请将S表示为θ的函数,并指出当点H在
上.设矩形AGHM的面积为S,∠HCF=θ,请将S表示为θ的函数,并指出当点H在 的何处时,该健身室的面积最大,最大面积是多少?
的何处时,该健身室的面积最大,最大面积是多少?
S=(50-40cosθ)(50-40sinθ),当θ=0或θ=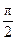 ,Smax=500
,Smax=500
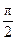 ,Smax=500
,Smax=500解: 延长GH交CD于N,则NH=40sinθ,CN=40cosθ.
∴HM=ND=50-40cosθ,AM=50-40sinθ.
故S=(50-40cosθ)(50-40sinθ)=
100[25-20(sinθ+cosθ)+16sinθcosθ](0≤θ≤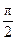 ).
).
令t=sinθ+cosθ=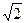 sin(θ+
sin(θ+ ),
),
则sinθcosθ=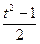 ,且t∈[1,
,且t∈[1,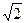 ].
].
∴S=100[25-20t+8(t2-1)]=800(t-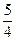 )2+450.
)2+450.
又t∈[1,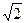 ],∴当t=1时,Smax=500,
],∴当t=1时,Smax=500,
此时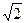 sin(θ+
sin(θ+ )=1
)=1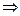 sin(θ+
sin(θ+ )=
)=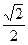 .
.
∵ ≤θ+
≤θ+ ≤
≤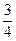 π,∴θ+
π,∴θ+ =
= 或
或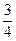 π,
π,
即θ=0或θ=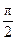 .
.
答:当点H在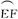 的端点E或F处时,该健身室的面积最大,最大面积是500 m2.
的端点E或F处时,该健身室的面积最大,最大面积是500 m2.
∴HM=ND=50-40cosθ,AM=50-40sinθ.
故S=(50-40cosθ)(50-40sinθ)=
100[25-20(sinθ+cosθ)+16sinθcosθ](0≤θ≤
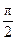 ).
).令t=sinθ+cosθ=
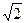 sin(θ+
sin(θ+ ),
),则sinθcosθ=
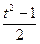 ,且t∈[1,
,且t∈[1,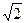 ].
].∴S=100[25-20t+8(t2-1)]=800(t-
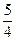 )2+450.
)2+450.又t∈[1,
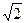 ],∴当t=1时,Smax=500,
],∴当t=1时,Smax=500,此时
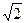 sin(θ+
sin(θ+ )=1
)=1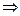 sin(θ+
sin(θ+ )=
)=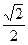 .
.∵
 ≤θ+
≤θ+ ≤
≤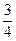 π,∴θ+
π,∴θ+ =
= 或
或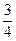 π,
π,即θ=0或θ=
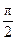 .
.答:当点H在
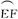 的端点E或F处时,该健身室的面积最大,最大面积是500 m2.
的端点E或F处时,该健身室的面积最大,最大面积是500 m2.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 R
R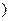 .
.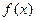 的最小正周期;
的最小正周期;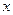 的值.
的值.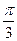 ―2x),
―2x),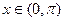 的单调增区间
的单调增区间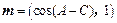 和
和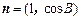 满足
满足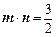 .
.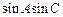 的值;
的值;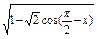 的定义域和值域.
的定义域和值域.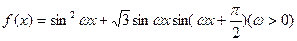
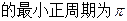 (1)求
(1)求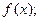
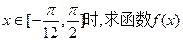 的值域。
的值域。 中,
中, ,
,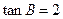 ,求
,求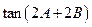 的值.
的值.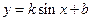 的最大值为
的最大值为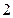 ,最小值为
,最小值为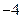 ,求
,求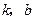 的值.
的值.