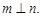题目内容
在正四棱柱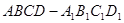 中,若
中,若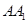 =
=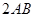 ,则异面直线
,则异面直线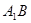 与
与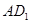 所成角的余弦值为 ( )
所成角的余弦值为 ( )
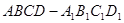 中,若
中,若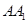 =
=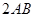 ,则异面直线
,则异面直线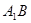 与
与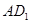 所成角的余弦值为 ( )
所成角的余弦值为 ( )A. | B. | C. | D. |
C
解:连接BC 、A
、A C
C
∵A D‖BC
D‖BC
∴∠A1BC1即相当于异面直线A B与AD
B与AD 所成角
所成角
在△BA1C1中,BA1=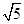 AB,A1C1=
AB,A1C1=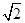 AB,C1B=
AB,C1B=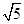 AB (1)
AB (1)
根据余弦定理可知:(A1C1)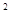 =(BA1)
=(BA1)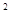 +(C1B)
+(C1B)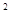 -2BA1·C1B·cos∠A
-2BA1·C1B·cos∠A BC
BC (2)
(2)
将(1)代入(2)求得:
cos∠A BC
BC =4/5
=4/5
即异面直线A B与AD
B与AD 所成角的余弦值为4/5
所成角的余弦值为4/5
 、A
、A C
C
∵A
 D‖BC
D‖BC
∴∠A1BC1即相当于异面直线A
 B与AD
B与AD 所成角
所成角在△BA1C1中,BA1=
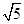 AB,A1C1=
AB,A1C1=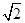 AB,C1B=
AB,C1B=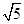 AB (1)
AB (1)根据余弦定理可知:(A1C1)
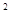 =(BA1)
=(BA1)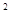 +(C1B)
+(C1B)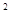 -2BA1·C1B·cos∠A
-2BA1·C1B·cos∠A BC
BC (2)
(2)将(1)代入(2)求得:
cos∠A
 BC
BC =4/5
=4/5即异面直线A
 B与AD
B与AD 所成角的余弦值为4/5
所成角的余弦值为4/5
练习册系列答案
相关题目
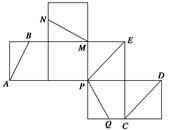
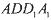 中,点B、C在线段AD上,且AB = 3,BC = 4,作
中,点B、C在线段AD上,且AB = 3,BC = 4,作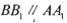 分别交
分别交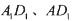 于点B,P,作
于点B,P,作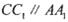 分别交
分别交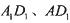 于点
于点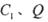 ,将该正方形沿
,将该正方形沿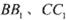 折叠,使得
折叠,使得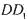 与
与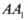 重合,构成如图2所示的三棱柱
重合,构成如图2所示的三棱柱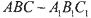
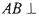 平面
平面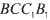 ;
;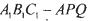 的体积.
的体积.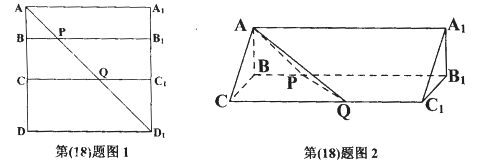
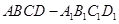 的顶点A作直线L,使L与棱
的顶点A作直线L,使L与棱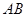 ,
,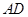 ,
,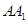 所成的角都相等,这样的直线L可以作( )
所成的角都相等,这样的直线L可以作( )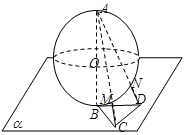
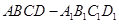 的棱
的棱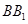 和
和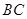 的中点分别是
的中点分别是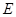 、
、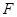 ,各棱所在直线中与直线
,各棱所在直线中与直线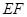 异面的直线条数是( )
异面的直线条数是( )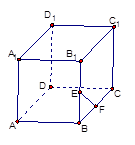
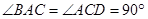 ,AE∥CD,DC=AC=2AE=2.
,AE∥CD,DC=AC=2AE=2. CD
CD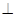 平面ABC
平面ABC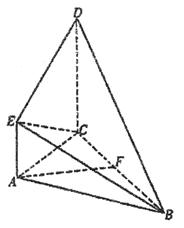
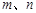 是不重合的直线,
是不重合的直线,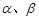 是不重合的平面,有下列命题:
是不重合的平面,有下列命题: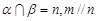 ,则
,则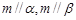 ;②若
;②若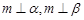 ,则
,则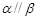 ;
;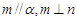 ,则
,则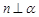 ; ④若
; ④若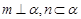 ,则
,则