Question

【题目】在平面直角坐标系xOy中，椭圆 + =1（a＞b＞0）的离心率为e，D为右准线上一点．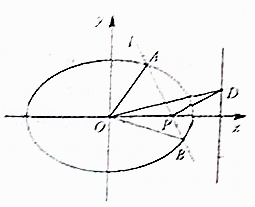

（1）若e= ，点D的横坐标为4，求椭圆的方程；
（2）设斜率存在的直线l经过点P（ ，0），且与椭圆交于A，B两点．若 + = ，DP⊥l，求椭圆离心率e．

Answer 1

【答案】
（1）

解：由椭圆的离心率e= = ，则a=2c，①椭圆的右准线方程x= ，

由 =4，则a2=4c，②，解得：a=2，c=1，

b2=a2﹣c2=3，

∴椭圆的标准方程：

（2）

解：方法一：设直线AB的方程：x=my+ ，A（x1，y1），B（x2，y2），

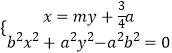，整理得：（a2+b2m2）y2+ ab2my﹣ a2b2=0，

y1+y2=﹣ ，则x1+x2=m（y1+y2）+ = ，

由 + = ，则 =（x1+x2，y1+y2）=（ ，﹣ ），

则D（ ，﹣ ），由D在椭圆的右准线上，则 = ，整理得3ac=2（a2+b2m2），

∴D（ ，﹣ ），则直线PD的斜率 =﹣ ，

由DP⊥l，则﹣ =﹣m，整理得4b2=4a2﹣3ac，即3ac=4（a2﹣b2）=4c2，则3a=4c，

∴椭圆的离心率e= = ，

椭圆离心率e的值为 ．

方法二：设D（ ，y），P（ ，0），则直线DP的斜率kPD= = ，

设A（x1，y1），B（x2，y2），由 + = ，则 ，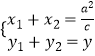

则 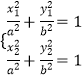，两式相减，整理得： =﹣ × =﹣ × =﹣ ，

∴直线l的斜率kAB=﹣ ，

∴DP⊥l，则kPDkAB=﹣1，

×（﹣ ）=﹣1，整理得4b2=4a2﹣3ac，即3ac=4（a2﹣b22，则3a=4c，

∴椭圆的离心率e= = ，

椭圆离心率e的值为

【解析】（1）由椭圆的离心率e= = ，a=2c，准线 =4，即可求得a和c，则b2=a2﹣c2=3，即可求得椭圆方程；（2）方法一：设直线l的方程，代入椭圆方程，利用韦达定理及向量的坐标运算，即可求得D点坐标，由D的横坐标为 ，即可表示出D点坐标，即可求得直线PD的斜率，由kPDkAB=﹣1，即可求得a和c的关系，即可求得椭圆离心率e；
方法二：设D点坐标，求得直线PD的方程，利用点差法及向量的数量积，即可求得直线AB的斜率，由kPDkAB=﹣1，即可求得a和c的关系，即可求得椭圆离心率e．