题目内容
【题目】已知正方体ABCD﹣A1B1C1D1 , O是底ABCD对角线的交点.求证: 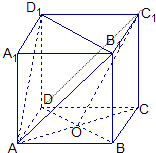
(1)C1O∥面AB1D1;
(2)面OC1D∥面AB1D1 .
【答案】
(1)解:由题意:几何体ABCD﹣A1B1C1D1是正方体,O是底ABCD对角线的交点,
∴B1D1∥BD,
连接A1C1交于O1,连接AO1,
![]() C1O1
C1O1
∴C1O1AO是平行四边形.
∴AO1∥C1O.
∵AO1面AB1D1;
∴C1O∥面AB1D1;
得证
(2)解:∵B1D1∥BD,即OD∥B1D1,
OD面OC1D,
∴OD∥面AB1D1.
由(1)可得C1O∥面AB1D1;
OD∩C1O=O,
所以:面OC1D∥面AB1D1.
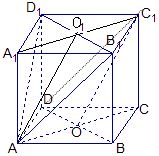
【解析】(1)线面平行,只需要证明线线平行.连接A1C1交于O1 . 连接AO1只需要证明AO1∥C1O即可.(2)面面平行,只需要证明一个平面内条的两条相交直线与平面平行即可,B1D1∥BD,AO1∥C1O,
BD∩C1O=O,那么可证得面OC1D∥面AB1D1 .
【考点精析】认真审题,首先需要了解直线与平面平行的判定(平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行),还要掌握平面与平面平行的判定(判断两平面平行的方法有三种:用定义;判定定理;垂直于同一条直线的两个平面平行)的相关知识才是答题的关键.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目