Question

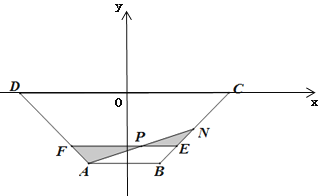
【题目】某市开发了一块等腰梯形的菜花风景区（如图）．经测量，长为百米，长为百米，与相距百米，田地内有一条笔直的小路（在上，在上）与平行且相距百米．现准备从风景区入口处出发再修一条笔直的小路与交于，在小路与的交点处拟建一座瞭望塔．

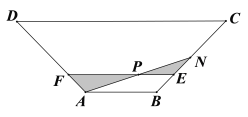
（1）若瞭望塔恰好建在小路的中点处，求小路的长；

（2）两条小路与将菜花风景区划分为四个区域，若将图中阴影部分规划为观赏区．求观赏区面积的最小值．

Answer 1

【答案】（1）百米；（2）（）平方百米．

【解析】

（1）过点P、N、C分别做AB的垂线，垂足分别为Q、M、G，在直角三角形AMN中，结合勾股定理，即可求解；

（2）以直线CD所在直线为轴，边CD的垂直平分线为轴建立如图所示的平面直角坐标系，设，得出面积，结合基本不等式，即可求解.

（1）过点P、N、C分别做AB的垂线，垂足分别为Q、M、G，

因为P是AN的中点，所以，

由已知条件易知是等腰直角三角形，所以，

所以，

在直角三角形AMN中，由勾股定理得，

答：小路AN的长为百米；

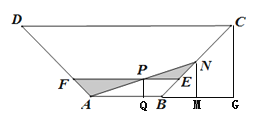
（2）以直线CD所在直线为轴，边CD的垂直平分线为轴建立如图所示的平面直角坐标系，

设，则直线，

联立直线，得，

所以的高为，

所以，

令，则，

所以当即时，S的最小值为．

答：观赏区面积的最小值为（）平方百米．