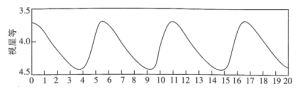
题目内容
【题目】设椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,上顶点为
,上顶点为![]() ,离心率为
,离心率为![]() , 在
, 在![]() 轴负半轴上有一点
轴负半轴上有一点![]() ,且
,且![]()
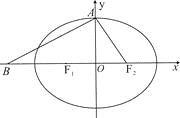
(1)若过![]() 三点的圆 恰好与直线
三点的圆 恰好与直线![]() 相切,求椭圆C的方程;
相切,求椭圆C的方程;
(2)在(1)的条件下,过右焦点![]() 作斜率为
作斜率为![]() 的直线
的直线![]() 与椭圆C交于
与椭圆C交于![]() 两点,在
两点,在![]() 轴上是否存在点
轴上是否存在点![]() ,使得以
,使得以![]() 为邻边的平行四边形是菱形,如果存在,求出
为邻边的平行四边形是菱形,如果存在,求出![]() 的取值范围;如果不存在,说明理由.
的取值范围;如果不存在,说明理由.
【答案】(1)![]() ;(2)存在满足题意的点
;(2)存在满足题意的点![]() 且
且![]() 的取值范围是
的取值范围是![]() .
.
【解析】
(1)根据![]() ,得
,得![]() ,所以|F1F2|=a,利用
,所以|F1F2|=a,利用![]() ,可得F1为BF2的中点,从而可得△ABF2的外接圆圆心为
,可得F1为BF2的中点,从而可得△ABF2的外接圆圆心为![]() ,半径r=|F1A|=a,根据过A、B、F2三点的圆与直线
,半径r=|F1A|=a,根据过A、B、F2三点的圆与直线![]() 相切,利用点到直线的距离公式,即可确定椭圆方程;
相切,利用点到直线的距离公式,即可确定椭圆方程;
(2)由(1)知F2(1,0),设l的方程为:y=k(x﹣1)与椭圆方程联立,利用韦达定理,结合菱形对角线垂直,所以![]() ,可得m,k之间的关系,从而可得结论.
,可得m,k之间的关系,从而可得结论.
(1)由题意![]() ,得
,得![]() ,所以|F1F2|=a,∵|AF1|=|AF2|=a,
,所以|F1F2|=a,∵|AF1|=|AF2|=a,![]() ,
,
∴F1为BF2的中点,∴|AF1|=|AF2|=|F1F2|=a,∴△ABF2的外接圆圆心为![]() ,半径r=|F1A|=a,
,半径r=|F1A|=a,
又过A、B、F2三点的圆与直线![]() 相切,所以
相切,所以 ,
,
∴a=2,∴c=1,b2=a2﹣c2=3.∴所求椭圆方程为![]() ;
;
(2)由(1)知F2(1,0),设l的方程为:y=k(x﹣1),
将直线方程与椭圆方程联立 ,整理得(3+4k2)x2﹣8k2x+4k2﹣12=0;
,整理得(3+4k2)x2﹣8k2x+4k2﹣12=0;
设M(x1,y1),N(x2,y2),则![]() ;
;
假设存在点P(m,0),使得以PM,PN为邻边的平行四边形是菱形,由于菱形对角线垂直,所以![]() ,
,
又![]()
又MN的方向向量是(1,k),故k(y1+y2)+x1+x2﹣2m=0,则k2(x1+x2﹣2)+x1+x2﹣2m=0,
即 ,由已知条件知k≠0且k∈R,
,由已知条件知k≠0且k∈R,
∴ ,∴
,∴![]() ,故存在满足题意的点P且m的取值范围是
,故存在满足题意的点P且m的取值范围是![]() .
.