题目内容
【题目】在直角坐标系xOy中，直线C1：x=﹣2以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，C2极坐标方程为：ρ2﹣2ρcosθ﹣4ρsinθ+4=0.
（1）求C1的极坐标方程和C2的普通方程；
（2）若直线C3的极坐标方程为
，设C2与C3的交点为M，N，又C1：x=﹣2与x轴交点为H，求△HMN的面积.
【答案】（1）C1的极坐标方程
，C2的普通方程
.（2）1
【解析】
（1）直接利用转换关系，把参数方程极坐标方程和直角坐标方程之间进行转换.
（2）利用一元二次方程根和系数关系和极径的应用求出结果.
（1）直线C1：x=﹣2，转换为极坐标方程为ρcosθ=﹣2.
C2极坐标方程为：ρ2﹣2ρcosθ﹣4ρsinθ+4=0，
转换为直角坐标方程为(x﹣1)2+(y﹣2)2=1.
（2）将
代入C2极坐标方程为：ρ2﹣2ρcosθ﹣4ρsinθ+4=0.得到
，解得
，
所以
，
由于H(﹣2，0)到直线y=x的距离为
，
所以S△HNM=1.
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
【题目】下表是某原料在市场上从2013年至2019年这7年中每年的平均价格（单位：千元/吨）数据：
年份 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
平均价格 （单位：千元/吨） |
|
|
|
|
|
|
|
（
和
线性相关性较强，求出以为解释变量为预报变量的线性回归方程（系数精确到
）；
（2）以（1）的结论为依据，预测2032年该原料价格.预估该原料价格在哪一年突破1万元/吨？
参考数据：
，
，
，
参考公式：回归方程
中斜率和截距的最小二乘估计公式分别为：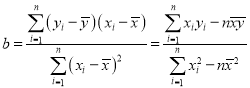
，
.
