题目内容
已知锐角 中的内角
中的内角 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、 ,定义向量
,定义向量 ,
, ,且
,且 .
.
(1)求 的单调减区间;
的单调减区间;
(2)如果 ,求
,求 的面积的最大值.
的面积的最大值.
(1)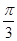 ;(2)
;(2)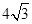
解析试题分析:(1)利用向量垂直,向的数量积为0得到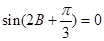 ,根据锐角三角形的内角
,根据锐角三角形的内角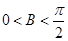 求角
求角 ,再由正弦函数
,再由正弦函数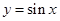 得单调减区间为
得单调减区间为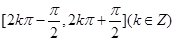 求解;(2)由余弦定理及三角形的面积公式求解.
求解;(2)由余弦定理及三角形的面积公式求解.
试题解析:∵ ,
,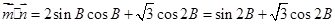
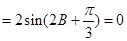 ,
,
∴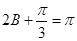 ,∴
,∴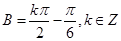 ,又
,又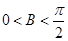 ,∴
,∴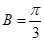 ,(4分)
,(4分)
(1)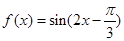 ,由
,由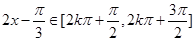 得:
得:
函数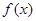 的单调减区间为
的单调减区间为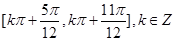 . (8分)
. (8分)
(2)由余弦定理知,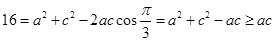 ,
,
∴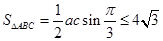 . (12分)
. (12分)
考点:向量的数量积,二倍角公式,余弦定理,三角形的面积公式.

练习册系列答案
相关题目
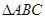 中,角
中,角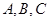 所对的边分别为
所对的边分别为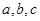 且
且 .
.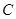 大小;
大小; ,向量
,向量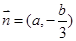 ,
,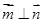 ,
, ,求
,求 ,
, .
. 的最小正周期及对称轴方程;
的最小正周期及对称轴方程; 时,求函数
时,求函数 (
( 为常数).
为常数). 的最小正周期和单调增区间;
的最小正周期和单调增区间; 个单位后,得到函数
个单位后,得到函数 的图像关于
的图像关于 轴对称,求实数
轴对称,求实数 的最小值.
的最小值.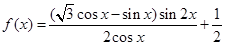 .
.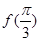 的值;
的值;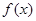 的最小正周期及单调递减区间.
的最小正周期及单调递减区间.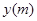 是时间
是时间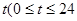 ,单位:
,单位: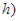 的函数,记作:
的函数,记作: ,下表是该港口在某季每天水深的数据:
,下表是该港口在某季每天水深的数据:
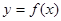 的曲线可以近似地看做函数
的曲线可以近似地看做函数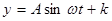 的图象.
的图象. 以上时认为是安全的(船舶停靠时,船底只需不碰到海底即可),某船吃水深度(船底离水面的距离)为
以上时认为是安全的(船舶停靠时,船底只需不碰到海底即可),某船吃水深度(船底离水面的距离)为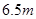 ,如果该船想在同一天内安全进出港,问它至多能在港内停留多长时间(忽略进出港所需时间)?
,如果该船想在同一天内安全进出港,问它至多能在港内停留多长时间(忽略进出港所需时间)?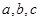 分别为三个内角
分别为三个内角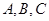 的对边,锐角
的对边,锐角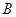 满足
满足 . (Ⅰ)求
. (Ⅰ)求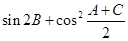 的值;
的值;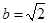 ,当
,当 取最大值时,求
取最大值时,求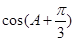 的值.
的值.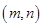 ,
,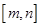 ,
,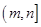 ,
,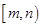 的长度均为
的长度均为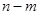 ,其中
,其中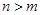 .
. 的不等式
的不等式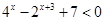 的解集构成的区间的长度;
的解集构成的区间的长度;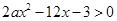 的解集构成的区间的长度为
的解集构成的区间的长度为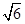 ,求实数
,求实数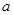 的值;
的值;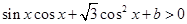 ,
,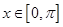 的解集构成的各区间的长度和超过
的解集构成的各区间的长度和超过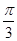 ,求实数
,求实数 的取值范围.
的取值范围.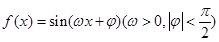 ,在同一个周期内,当
,在同一个周期内,当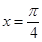 时
时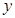 取最大值1,当
取最大值1,当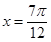 时,
时, ;
; 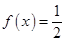 ;求在
;求在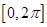 内的所有实数根之和.
内的所有实数根之和.